Spiral of Theodore
In geometry, the spiral of Theodorus (also called square root spiral, Einstein spiral or Pythagorean spiral) is a spiral composed of right triangles, placed edge-to-edge. It was named after Theodorus of Cyrene.
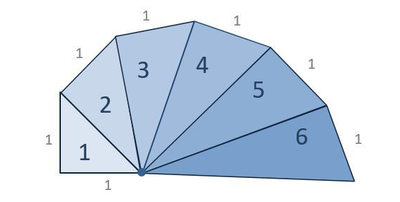
Which triangle has an area of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We note that the hypotenuse of the n th right triangle of Theodorus spiral is h n = n + 1 . And h n = b n + 1 the base of the ( n + 1 ) th right triangle. Therefore the area of the n th right triangle is A n = 2 n . And for A n = 1 , we have 2 n = 1 ⟹ n = 4 .