Spiral of Theodorus
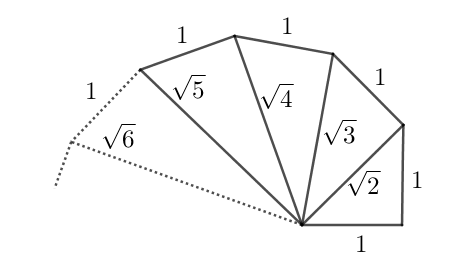
If you continued the spiral, what would be the value of the last hypotenuse before the triangles start to overlap?
If the value is , express it as .
The answer is 4123.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The sum of the angles of the concurrent vertices is:
φ ( n ) = k = 1 ∑ n arctan k 1 = 2 n + c 2 ( n ) , where lim n → ∞ c 2 ( n ) ≈ − 2 . 1 5 7 7 8 3
The following is a plot of how the correction term c 2 ( n ) varies with n for the first 20 values of n :
2 1 6 + c 2 ( 1 6 ) ≈ 6 . 1 2 8 7 3 1 ≤ 2 π ⟹ n m a x = 1 6 .
Therefore, h = 1 6 + 1 and ⌊ 1 0 0 0 h ⌋ = 4 1 2 3 .