Spiral table 2021
The Table is formed, using the spiral notation of integers (see figure). The sum of S ( n ) numbers in yellow cells for each n is calculated. Find the minimum value of n at which the sum S ( n ) is divisible by 2 0 2 1 .
S ( 1 ) = 1 , S ( 2 ) = 1 3 , . . . , S ( 9 ) = 1 0 8 2 1 , . . . .
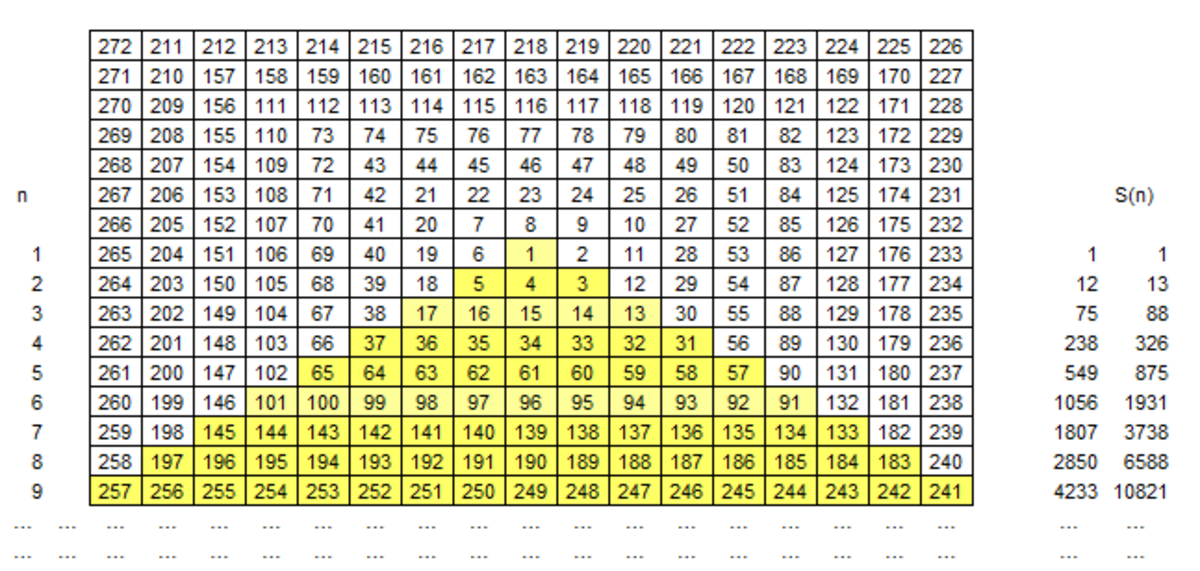
Give answer n .
The answer is 774.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thank for attention. Fine solution. There is interpolation polynomial for S(n) with power 4 - Wolframalpha . Happy New Year!
I had basically the same solution, except I looked first at the central column of numbers 1 , 4 , 1 5 , 3 4 , … ; these have the form 4 n 2 − 9 n + 6 . This will be the average value of the 2 n − 1 numbers in the n th row, so the row total is ( 2 n − 1 ) ( 4 n 2 − 9 n + 6 ) .
This doesn't help much with the final part of the question, which I did the same way. It's slightly quicker to factorise first, 2 0 2 1 = 4 3 × 4 7 (remember that fact, I bet it'll come up a lot this year!), then use the Chinese remainder theorem, but I still couldn't see a way to solve it by hand.
Log in to reply
Thanks for attention. I write problem for #ComputeSience, but @brilliant change to #Probability.
I don't think this can be solved by hand alone. This reminds me of Ulam's spiral .
Looking at the numbers formed from the right diagonal 1 , 3 , 1 3 , 3 1 , … tells us that it follows the sequence { a n } n ⩾ 1 = 4 n 2 − 1 0 n + 7 .
Looking at the numbers formed from the left diagonal 1 , 5 , 1 7 , 3 7 , 6 5 , … tells us that it follows the sequence { b n } n ⩾ 1 = 4 ( n − 1 ) 2 + 1 .
I'll leave the proof of these sequences as an exercise for the readers.
Thus, the n th row consists of N = 2 n − 1 integers, 4 ( n − 1 ) 2 + 1 , 4 ( n − 1 ) 2 , 4 ( n − 1 ) 2 − 1 , … , 4 n 2 − 1 0 n + 7
which follows an arithmetic progression , and the sum of each row is 2 N [ 2 a + ( N − 1 ) d ] = 2 2 n − 1 [ 2 [ 4 ( n − 1 ) 2 + 1 ] + ( 2 n − 2 ) ( − 1 ) ] = ( 2 n − 1 ) ( 4 n 2 − 9 n + 6 )
Hence, S ( n ) = k = 1 ∑ n ( 2 k − 1 ) ( 4 k 2 − 9 k + 6 ) = 6 n ( 1 2 n 3 − 2 0 n 2 + 9 n + 5 )
by invoking sum of powers . We want to find min ( n ) such that S ( n ) is divisible by 2021.
Running a simple script tells us that the answer is 7 7 4 . I'm interested to see a non-computer assisted solution.