Splattered paint
Maya randomly splatters four colors of paint across a canvas:
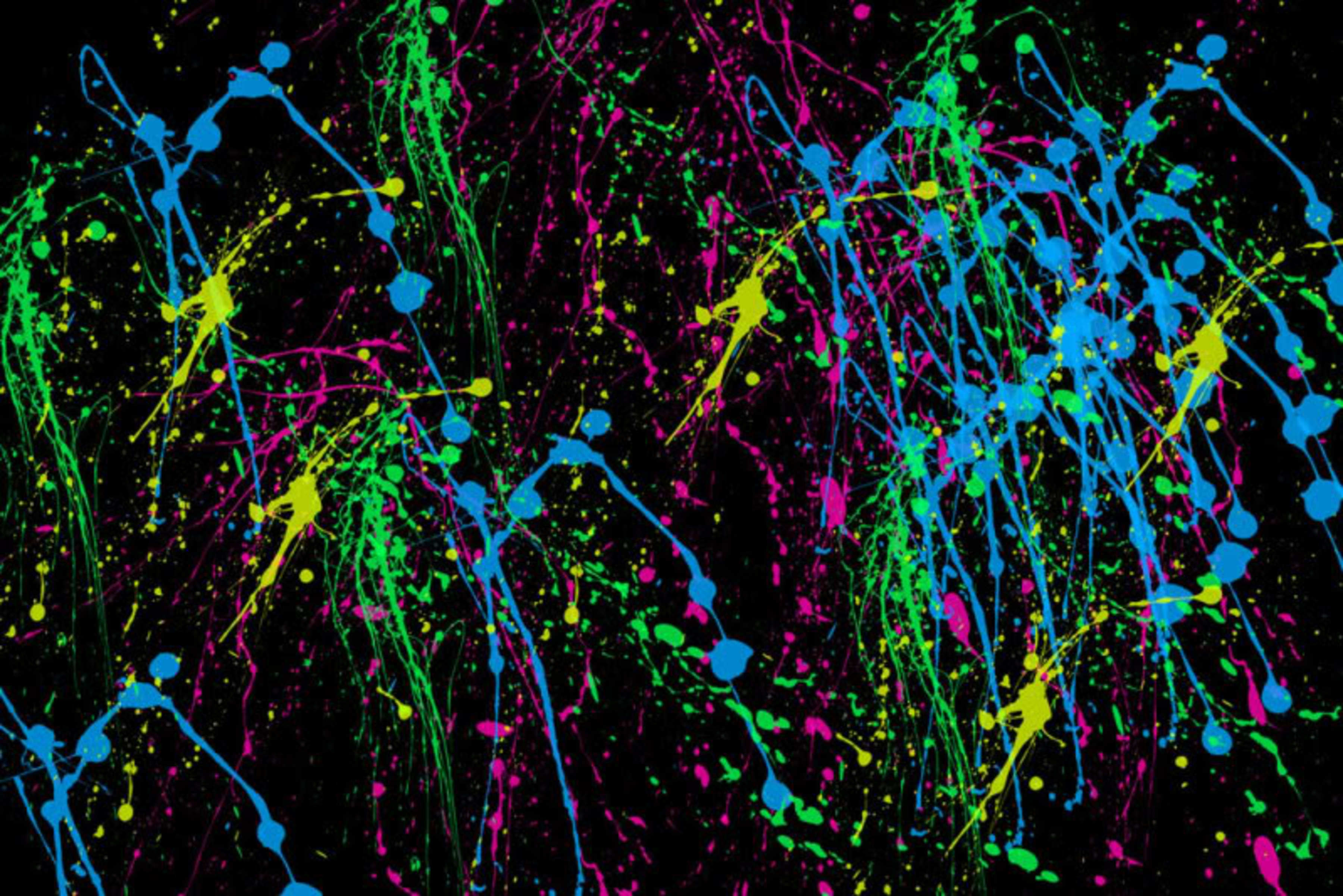
Then she decides to cut the canvas into two pieces with a straight cut, such that:
- There is the same area of yellow on one piece as there is green on the other piece.
- There is the same area of magenta on one piece as there is blue on the other piece.
Is there any way she can do this?
Image credit: https://www.pinterest.com
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
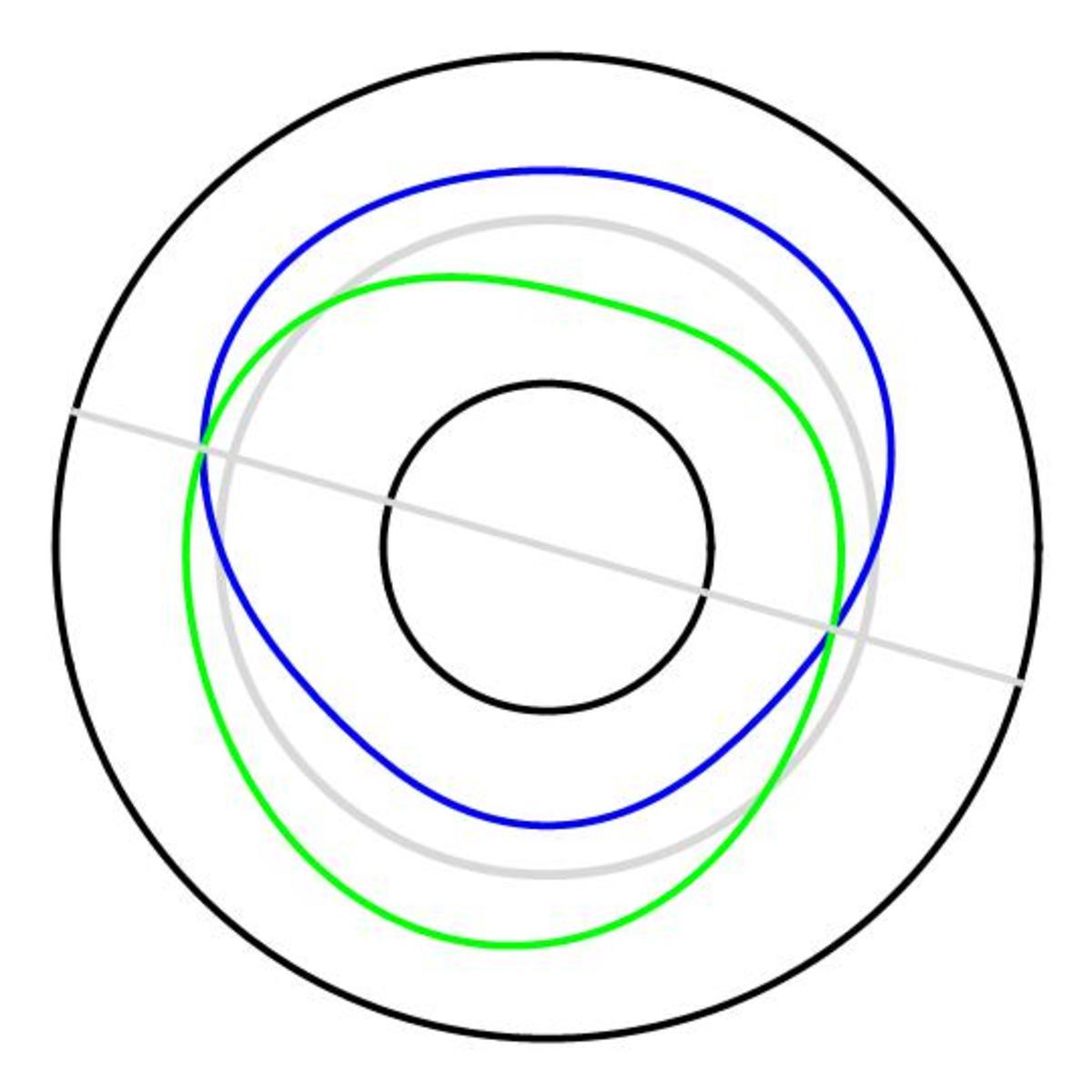
A partial solution:
Consider a vertical line swiped from the left to the right. Slowly the amount of yellow on the left side will increase from zero to the total yellow area, and the amount of green on the right size will decrease from the total green area to zero. At some point they will meet, and the amount of yellow on the left side will be the same as the amount of green on the right side. Note : The orientation (vertical) we chose for the line was arbitrary, so WLOG any angle could have been chosen.
The same argument holds for magenta and blue.
In general, the place where the green/yellow and magenta/blue lines meets will be different for a different orientation.
However, as the orientation is rotated from 0 ∘ to 3 6 0 ∘ , at some point, the lines will meet in the same place for the green/yellow combo as it does for the magenta/blue combo. Now, to come up with a more rigorous proof as to why this is so... Stay tuned!