Split Disk Moment
Consider a solid, uniform circular disk of mass and radius , with its center at . The disk resides within the plane.
Each point on the disk can be represented in polar coordinates as , where is the distance from the origin (not from the center of the disk) and is the angle with respect to the positive axis.
Let us move each infinitesimal bit of mass on the disk from to , where for and for . The resulting mass arrangement is as shown in the diagram.
What is the moment of inertia of this split disk with respect to the axis?
Note: The mass of each infinitesimal portion is preserved as it is moved.
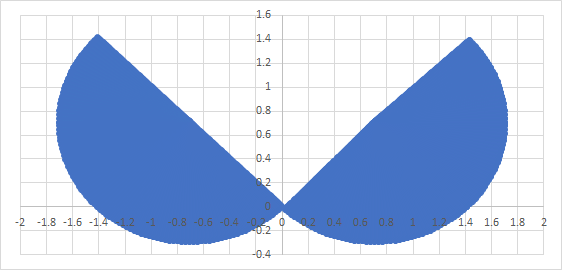
The answer is 1.175.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's denote the right half of the "nutmeg" by D and proceed in polar coordinates. The moment of inertia we seek is 2 ∫ ∫ D x 2 d m = π 2 ∫ ∫ D x 2 d A = π 2 ∫ − 4 π 4 π ∫ 0 2 sin ( θ + 4 π ) r 3 cos 2 θ d r d θ = 4 3 + 3 π 4 ≈ 1 . 1 7 4 4