Split Parabola

Calculus Level 4

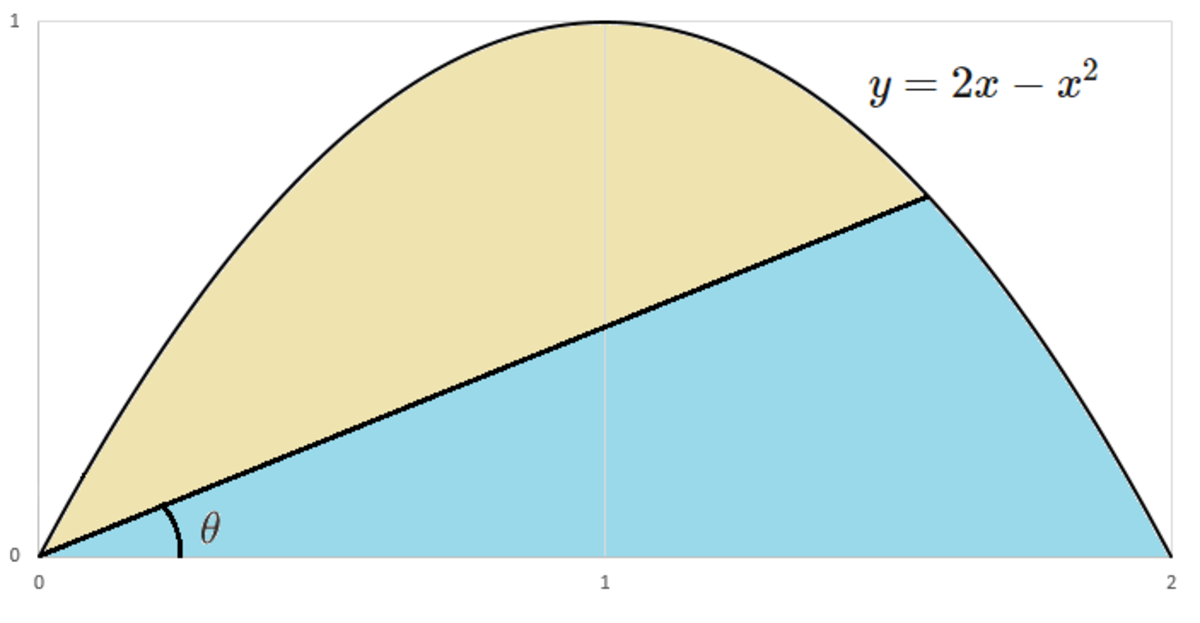
Consider the region in the $xy$ plane bounded by the curve $y = 2x - x^2$ and the $x$ -axis.

Suppose we draw a line segment from the origin to a point on the curve, such that the region is divided into two parts of equal areas.

What angle $\theta$ does the line segment make with the $x$ -axis? Give your answer in degrees to 3 decimal places.

1 solution

Brandon Monsen
Sep 25, 2017

Let $f(x)=2x-x^{2}$ , and let the line drawn intersect the parabola at $x=a$ , where $a>0$ . Then we can express the conditions of the problem as

$\frac{1}{2} \int_{0}^{2} f(x) \ dx = \int_{0}^{a} \left[ f(x) - \frac{f(a)}{a}x \right] \ dx$

Which is saying that half the total area under the parabola is the area of the region bounded by our line and the parabola. This evaluates to

$\frac{2}{3} = \frac{1}{6}a^{3} \rightarrow a = \sqrt[3]{4}$

Now, our angle made with the x-axis is

$\theta = \tan^{-1} \left( \frac{2a-a^{2}}{a} \right) = \tan^{-1}(2-a) = 22.421^{o}$