Splitting a Hyperboloid

Geometry Level 4

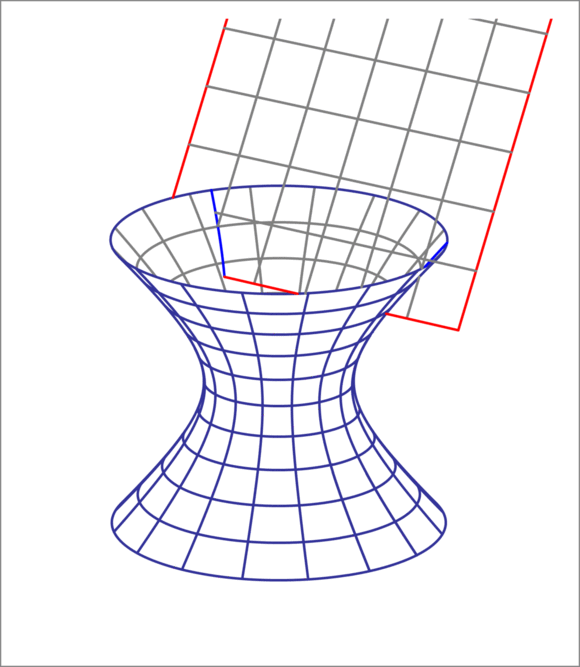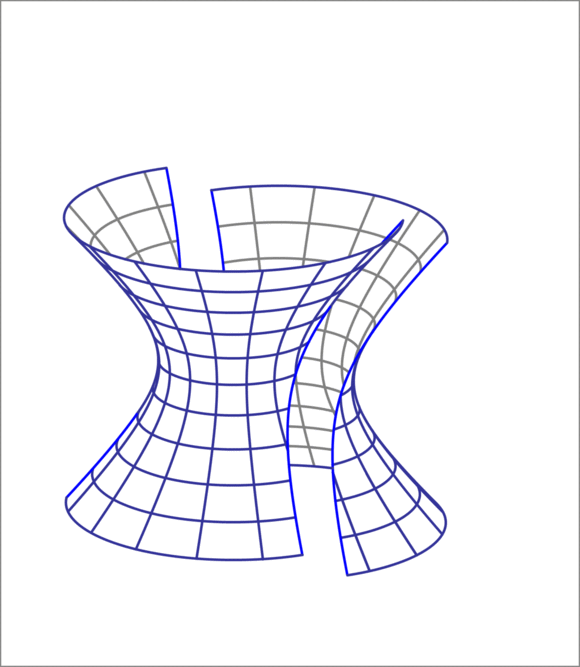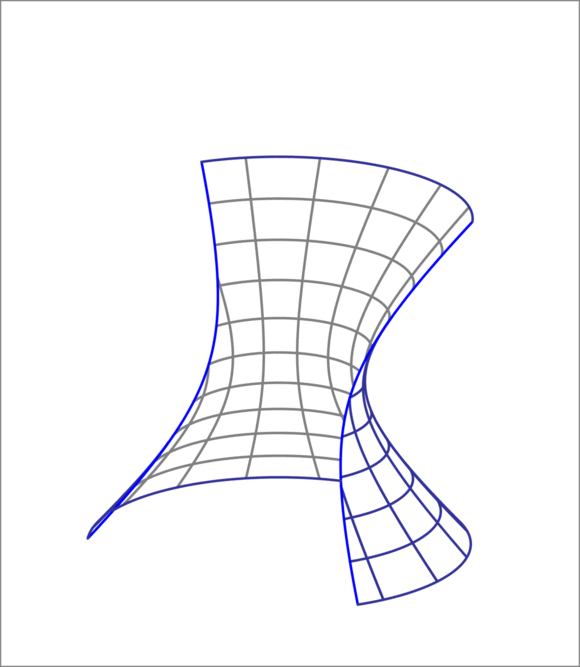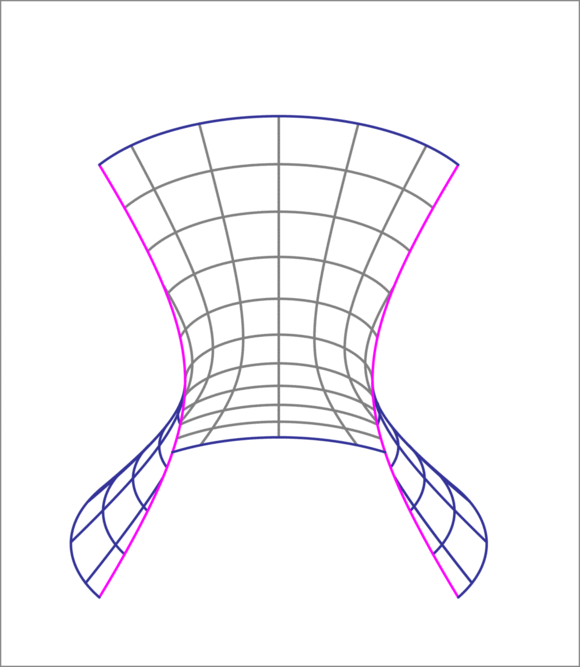
A hyperboloid of one sheet is given by

$\dfrac{x^2}{5^2} + \dfrac{y^2}{5^2} - \dfrac{z^2}{5^2} = 1$

You pass a plane having the normal vector $(\sqrt{3}, 0, 1)$ and passing through the origin $(0, 0, 0)$ , through the hyperboloid, and intersecting it in the hyperbola

$\dfrac{x'^2}{a^2} - \dfrac{y'^2}{b^2} = 1$

where the frame $O'x'y'z'$ is an isometry (i.e. equal scale) of the frame $Oxyz$ . Given that $a = n$ and $b = n \sqrt{m}$ , for some positive integers $n$ and $m$ , find $n + m$ .

The answer is 7.

1 solution

Hosam Hajjir
Nov 18, 2019

Points on the cutting plane are spanned by any two linearly independent vectors that are orthogonal to the normal to the plane. To generate a reference frame, we'll select these two vectors to be unit vectors and orthogonal to each other.

So, let $u_1 = (0, 1, 0)$ and $u_2 = ( -\dfrac{1}{2}, 0, \dfrac{\sqrt{3}}{2} )$ , then it follows that any point on the cutting plane can be written as

$p = x' u_1 + y' u_2 = ( -\dfrac{1}{2} y' , x', \dfrac{\sqrt{3}}{2} y' )$

Plugging in the coordinates of $p$ into the equation of the hyperboloid, we get,

$\dfrac{1}{4} y'^2 + x'^2 - \dfrac{3}{4} y'^2 = 25$

Simplifying and re-arranging, this becomes,

$\dfrac{x'^2}{25} - \dfrac{y'^2}{50} = 1$

Therefore, $a = 5$ , and $b = 5 \sqrt{2}$ , and this makes the answer $5 + 2 = \boxed{7}$

Splitting a Hyperboloid

The answer is 7.

1 solution

0 pending reports