Splitting a Parabolic Sheet
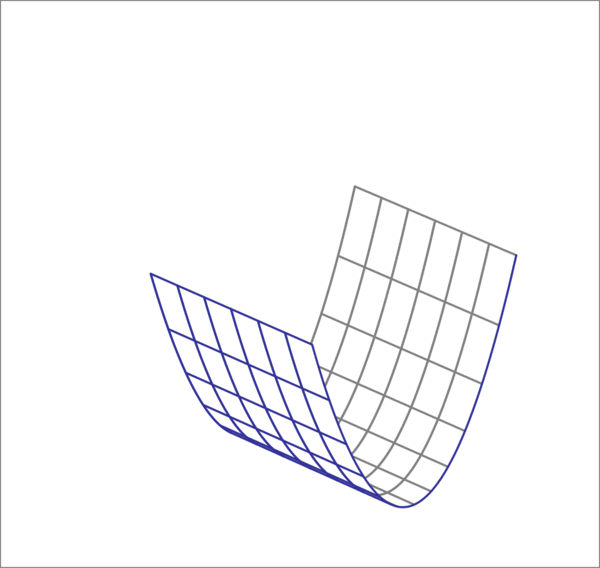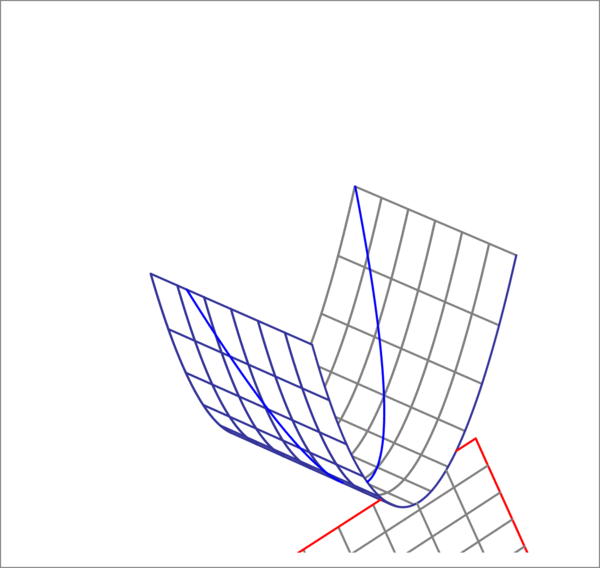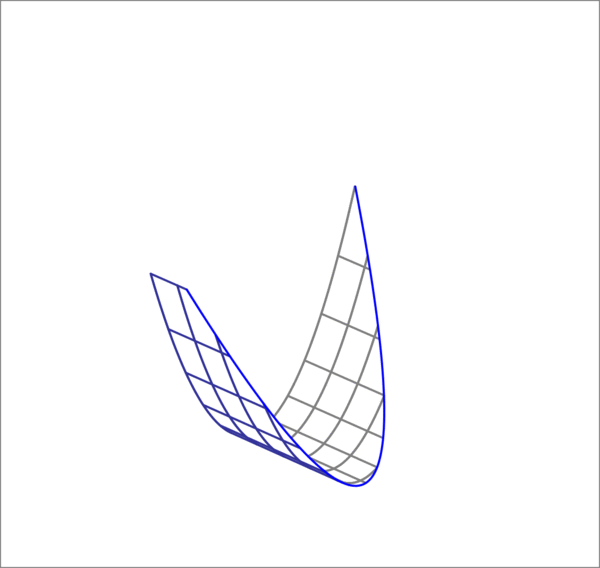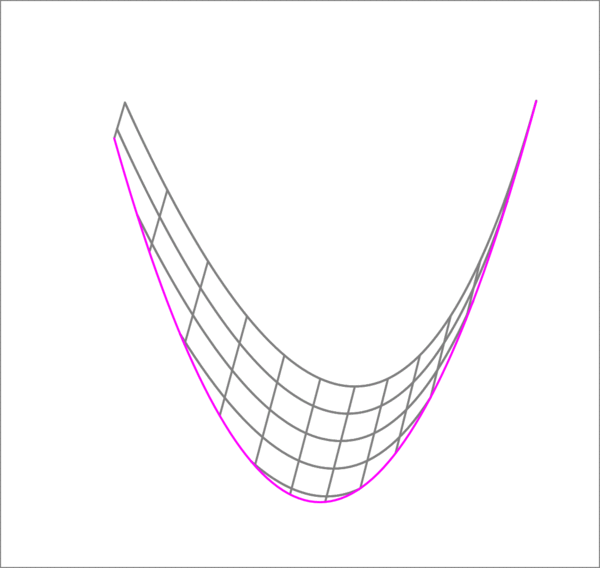
A parabolic sheet is given by
You pass a plane having the normal vector , with and passing through , through the parabolic sheet, and intersecting it in the parabola
where the frame is an isometry (i.e. equal scale) of the frame , and . Find .
The answer is 0.2832.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of the given parabolic sheet is
0 . 2 5 y 2 − z = 0
Define
r = [ x , y , z ] T
Then the equation of the parabolic sheet can be written as
r T Q r + b T r = 0
where
Q = ⎣ ⎡ 0 0 0 0 0 . 2 5 0 0 0 0 ⎦ ⎤ and b = ⎣ ⎡ 0 0 − 1 ⎦ ⎤
On the other hand, a point in the cutting plane can be written in parametric form as
r = r 0 + V u
where r 0 is the position vector of any point on the plane, and can be taken as ( 2 , 0 , 0 ) , and matrix V is composed of two columns of two vectors v 1 and v 2 that are perpendicular to the normal vector to the plane. Further we will take v 1 and v 2 to be perpendicular to each other and to be of unit length.
The normal to the given plane is
n ^ = [ sin θ cos ϕ , sin θ sin ϕ , cos θ ] T
So we can take,
v 1 = [ − sin ϕ , cos ϕ , 0 ]
and
v 2 = n ^ × v 1 = [ − cos θ cos ϕ , − cos θ sin ϕ , sin θ ]
Now we can substitute the equation of the plane into the equation of the parabolic sheet
( r 0 + V u ) T Q ( r 0 + V u ) + b T ( r 0 + V u ) = 0
Expanding
r 0 T Q r 0 + u T V T Q V u + 2 u T V T Q r 0 + b T r 0 + b T V u = 0
Rearranging
u T V T Q V u + u T ( 2 V T Q r 0 + V T b ) = − r 0 T Q r 0 − b T r 0
Next, we diagonalize the matrix V T Q V , so that it can written as V T Q V = R D R T , with matrix R being an orthonormal matrix of unit eigenvectors.
And the above equation becomes,
u T R D R T u + u T ( 2 V T Q r 0 + V T b ) = − r 0 T Q r 0 − b T r 0
By choosing the columns of R appropriately, we can make the first entry on the diagonal of the diagonal matrix D nonzero, and the second entry zero.
Now define the vector w = R T u , then
w T D w + w T R T ( 2 V T Q r 0 + V T b ) = − r 0 T Q r 0 − b T r 0
This equation is of the form,
D 1 1 w 1 2 + α w 1 + β w 2 = γ
So, by completing the square, it becomes,
D 1 1 ( w 1 + 2 D 1 1 α ) 2 + β w 2 = γ + 4 D 1 1 α 2
This is an equation of a parabola, to put it the form given in the problem, we just shift the origin of the coordinate system to the vertex.
Define z = w + w 0 , where w 0 T = [ 2 D 1 1 α , − β 1 ( γ + 4 D 1 1 α 2 ) ]
Then,
D 1 1 z 1 2 + β z 2 = 0
Therefore, the required parameter a is given by a = − β D 1 1 .
Evaluating all of the above, yields
R = [ 0 . 9 9 6 1 3 6 1 1 − 0 . 0 8 7 8 2 2 8 3 6 0 . 0 8 7 8 2 2 8 3 6 0 . 9 9 6 1 3 6 1 1 ]
D = [ 0 . 2 4 4 3 4 6 1 8 3 0 0 0 ]
α = 0 . 0 7 6 0 5 6 8 0 7
β = − 0 . 8 6 2 6 7 9 1 7 7
γ = 0
Therefore,
a = − ( − 0 . 8 6 2 6 7 9 1 7 7 ) 0 . 2 4 4 3 4 6 1 8 3 = 0 . 2 8 3 2