Splitting A B 2 + A C 2 = B C 2
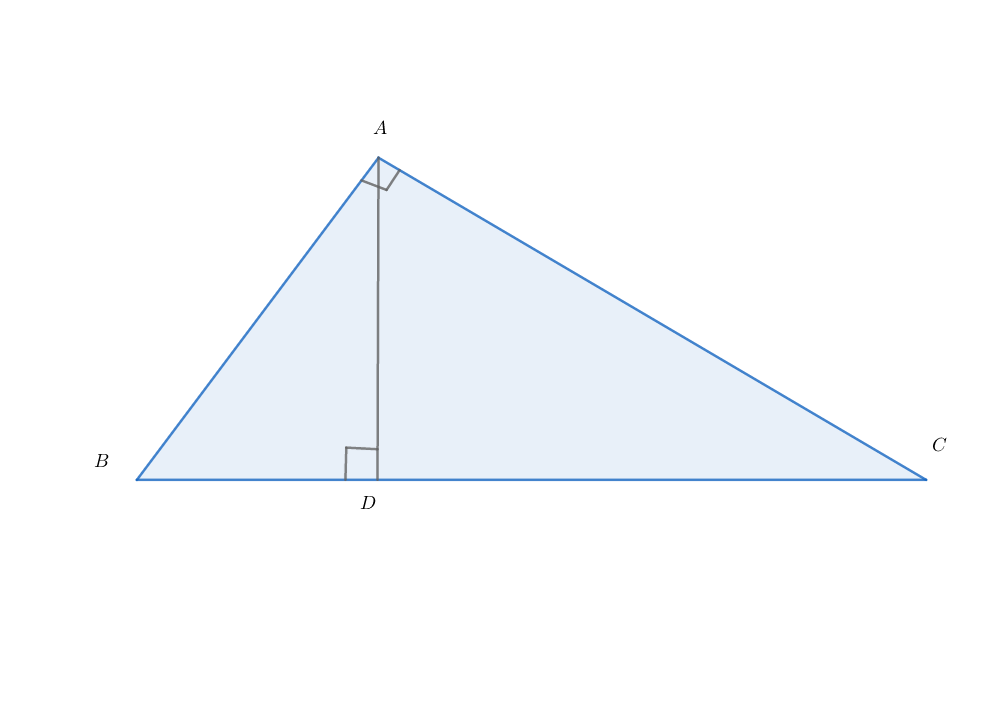
∠ B A C = ∠ A D C = ∠ A D B = 9 0 ∘ and A B = 2 4 , B D = 3 .
A C can be expressed as a b , where a and b are positive integers, and b is square-free.
Find ( a + b ) .
The answer is 79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The famous Pythagorean Theorem tells us A B 2 + A C 2 = B C 2 .
So, we can say─
A B 2 + A C 2 = B C ⋅ B C
⟹ A B 2 + A C 2 = B C ⋅ B C
⟹ A B 2 + A C 2 = B C ⋅ ( B D + C D )
⟹ A B 2 + A C 2 = B C ⋅ B D + B C ⋅ C D
Now let's split-up the last equality. Do the following equalities hold? A B 2 = B C ⋅ B D A C 2 = B C ⋅ C D
Yes, they hold (when A D ⊥ B C ).
- From the similarity between Δ A B C and Δ D B A , we have
B D A B = A B B C , which proves A B 2 = B C ⋅ B D
- Similarly, one can prove . A C 2 = B C ⋅ C D from the similarity between Δ A B C and Δ D C A ,
Now, As A B 2 = B C ⋅ B D , we get B C = B D A B 2 = 3 2 4 2 = 1 9 2 .
So, A C = B C 2 − A B 2 = 1 9 2 2 − 2 4 2 = 3 6 2 8 8 = 2 6 ⋅ 3 4 ⋅ 7 = 2 3 ⋅ 3 2 7 = 7 2 7 = a b .
Therefore, a = 7 2 , b = 7 with a + b = 7 9 .
First we observe that △ A B C ∼ △ A B D because their angles are congruent. Then, we can find the following relationship:
A B B D = A C A D
To find the length of A D we use the Pythagorean Theorem:
B D 2 + A D 2 = A B 2
3 2 + A D 2 = 2 4 2
9 + A D 2 + 5 7 6
A D = 5 6 7 = 3 4 ⋅ 7 = 9 7
Now we can find the length of A C :
A B B D = A C A D
2 4 3 = A C 9 7
3 ⋅ A C = 2 4 ⋅ 9 7
A C = 7 2 7
Since this answer is in its reduced form and the problem asks for a + b from a value in the form a b , the answer you should input is 7 2 + 7 = 7 9