Splitting Them Up!!

Geometry Level 5

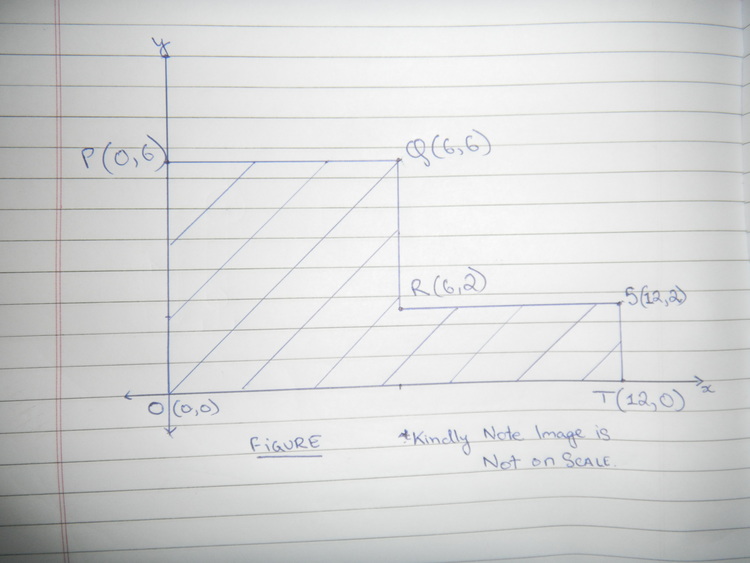In The Diagram,

Two Straight Lines Through O ( 0 , 0 ) O(0,0) ,

So That The Lines Divide the Figure O P Q R S T OPQRST in 3 3 Pieces Of Equal Area.

If the Sum of Slope Of these Lines can be Expressed as m n \dfrac{m}{n} ,where m , n m,n Are Co-Prime.

Find m + n \space m+n .


The answer is 19.

Vraj Mehta by Vraj Mehta , 30, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

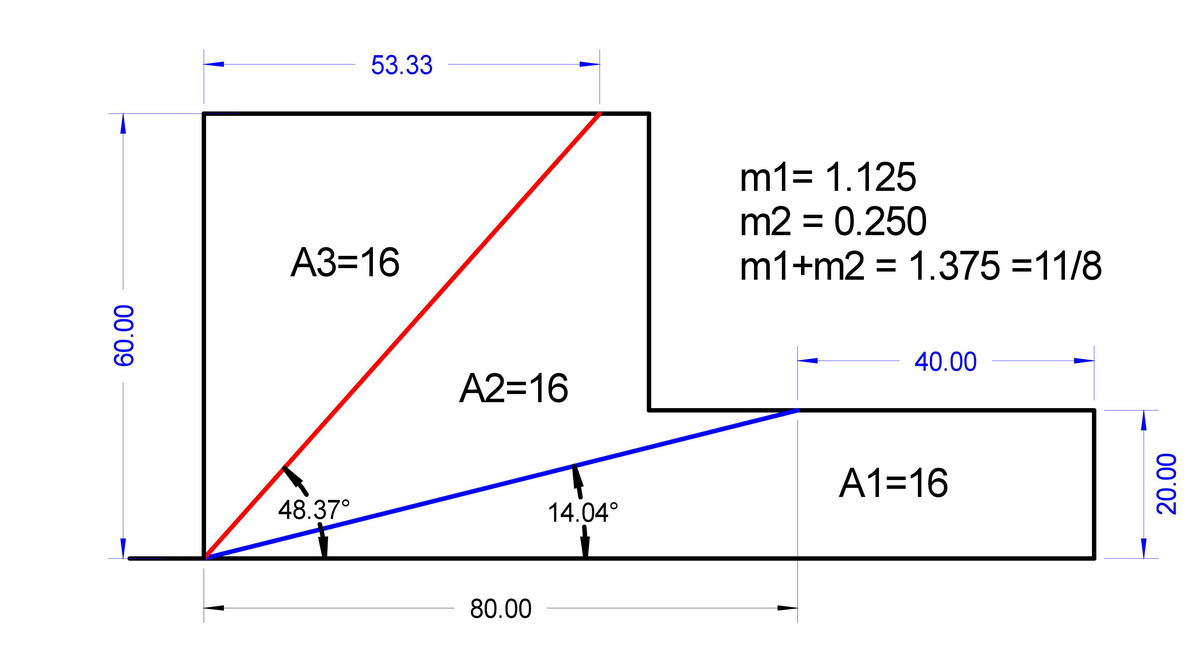
Nothing special. The problem seems overrated. The total area is 48 . The area of each part =48/3=16. So the area of triangle OPX is =16, and sides OP=6, and PX. ∴ 16 = 1 2 ∗ 6 ∗ P X ⟹ P X = 16 3 , X ( 16 3 , 6 ) a n d t h e s l o p e S 1 = 9 8 . T h e a r e a o f Δ S O T = 1 2 ∗ O T ∗ S T = 1 2 ∗ 12 ∗ 2 = 12. this is 16 - 12 = 4 short. So we add Δ Y O S , a r e a 4. ⟹ 4 = 1 2 ∗ Y S ∗ h e i g h t = 1 2 ∗ Y S ∗ 2. ∴ Y S = 4. ⟹ Y ( 12 − 4 , 2 ) = Y ( 8 , 2 ) a n d t h e s l o p e S 2 = 2 8 . S 1 + S 2 = 11 8 = m n . ∴ m + n = 19 \therefore~16=\dfrac 1 2 * 6 *P X~~ \implies~PX= \dfrac {16}{3},~~~ X(\dfrac {16}{3},6)~and ~the~slope~\color{#3D99F6}{S_1=\dfrac 9 8} .\\ The ~area~ of~ \Delta~SOT=\dfrac 1 2 *OT*ST=\dfrac 1 2 *12*2=12.\\\text {this is 16 - 12 = 4 short. So we add } ~\Delta~YOS,~area~4.\\\implies~4=\dfrac 1 2 *YS*height=\dfrac 1 2 *YS*2.~~\therefore~YS=4.\\\implies~Y(12-4,2)=Y(8,2) ~and ~the~slope~\color{#3D99F6}{S_2=\dfrac 2 8} .\\S_1+S_2=\dfrac {11} 8=\dfrac m n .~~~~\therefore~m+n=~~\color{#D61F06}{19}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Nothing special just dividing the total area 48units in three pieces, a triangle of are 16 units, a trapezium of 16 and the remain irregular polygon has to value 16 also

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Yup, the problem seems overrated. The key is to identify that the Blue line must intersect the middle horizontal line rather than the middle vertical line. Similarly, the Red line must intersect the top horizontal line rather than the middle vertical line... Afterwards, finding the slope is a matter of solving for the intersection points by equating areas of section A 1 A_1 and A 3 A_3 respectively...

Pawan Kumar - 6 years, 2 months ago

Yeah... The problem is overrated.. The main part was to identify the trapezing with one point (8,2)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...