Spooky Spooky Spooky

Level pending

x = t − sin ⁡ ( t ) , y = 1 − cos ⁡ ( t ) + 0.5 ∣ t ∣ , − 3 π < t < 3 π x = t - \sin(t), y = 1 - \cos(t) + 0.5\left|t\right|, \hspace{.2cm} -3\pi < t < 3\pi

x = t − sin ⁡ ( t ) , y = 4.1 + 0.5 cos ⁡ ( t ) + 0.33 ∣ t ∣ , − 3 π < t < 3 π x = t - \sin(t), y = 4.1 + 0.5\cos(t) + 0.33\left|t\right|, \hspace{.2cm} -3\pi < t < 3\pi

y = 0.5 ∣ x ∣ + 6.2 , − 1 < x < 1 y = 0.5\left|x\right| + 6.2, \hspace{.2cm} -1 < x < 1

y = 2 x 4 + 4.7 , − 1 < x < 1 y = 2x^4 + 4.7, \hspace{.2cm} -1 < x < 1

What creepy shape do the graphs of the equations above trace out? You might want to use a graphing tool for this one!

Ghost Mummy Witch Bat

View wiki
Andrew Ellinor by Andrew Ellinor , 33, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Andrew Ellinor
Oct 29, 2015

Here's what a plot of this guy looks like:

If that's not a scary looking bat \boxed{\text{bat}} , then I don't know what is.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Plot this:

( ( x 7 ) 2 ∣ ∣ x ∣ − 3 ∣ ∣ x ∣ − 3 + ( x 3 ) 2 ∣ y + 3 33 7 ∣ y + 3 33 7 − 1 ) ⋅ ( ∣ x 2 ∣ − ( 3 33 − 7 112 ) x 2 − 3 + 1 − ( ∣ ∣ x ∣ − 2 ∣ − 1 ) 2 − y ) ⋅ ( 9 ∣ ( ∣ x ∣ − 1 ) ( ∣ x ∣ − . 75 ) ∣ ( 1 − ∣ x ∣ ) ( ∣ x ∣ − . 75 ) − 8 ∣ x ∣ − y ) ⋅ ( 3 ∣ x ∣ + . 75 ∣ ( ∣ x ∣ − . 75 ) ( ∣ x ∣ − . 5 ) ∣ ( . 75 − ∣ x ∣ ) ( ∣ x ∣ − . 5 ) − y ) ⋅ ( 2.25 ∣ ( ∣ x ∣ − . 5 ) ( ∣ x ∣ + . 5 ) ∣ ( . 5 − ∣ x ∣ ) ( . 5 + ∣ x ∣ ) ) ⋅ ( 6 10 7 + ( 1.5 − . 5 ∣ x ∣ ) ∣ ∣ x ∣ − 1 ∣ ∣ x ∣ − 1 − 6 10 14 4 − ( ∣ x ∣ − 1 ) 2 − y ) = 0 \left( \left(\frac{x}{7}\right)^2 \sqrt{\frac{||x|-3|}{|x|-3}} + \left(\frac{x}{3}\right)^2 \sqrt{\frac{|y+\frac{3\sqrt{33}}{7}|}{y+\frac{3\sqrt{33}}{7}}} -1 \right) \cdot \left( |\frac{x}{2}| - \left(\frac{3\sqrt{33}-7}{112}\right)x^2 -3 + \sqrt{1-(||x|-2|-1)^2}-y \right) \\ \cdot \left( 9 \sqrt{\frac{|\left(|x|-1\right)\left(|x|-.75 \right)|}{\left(1-|x|\right) \left(|x|-.75\right)}} -8|x|-y \right) \cdot \left( 3|x|+.75 \sqrt{\frac{|\left(|x|-.75\right)\left(|x|-.5\right)|}{\left(.75-|x|\right)\left(|x|-.5 \right)}}-y \right) \\ \cdot \left(2.25 \sqrt{\frac{|\left(|x|-.5\right)\left(|x|+ .5\right)|}{\left(.5-|x|\right)\left(.5+|x|\right)}} \right) \cdot \left( \frac{6\sqrt{10}}{7} + \left(1.5 - .5|x|\right) \sqrt{\frac{||x|-1|}{|x|-1}} - \frac{6\sqrt{10}}{14} \sqrt{4-\left(|x|-1\right)^2}-y \right) = 0

Patrick Engelmann - 5 years, 7 months ago
Arnab Sen
Nov 1, 2015

matlab code : t=-3 pi:0.001:3 pi; x1=t-sin(t); y1=1-cos(t)+0.5 abs(t); x2=x1; y2=4.1+0.5 cos(t)+0.33 abs(t); x=-1:0.001:1; y3=0.5 abs(x)+6.2; y4=(2*x.^4)+4.7; plot(x1,y1,x2,y2,x,y3,x,y4)

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Axel Ordóñez
Nov 1, 2015

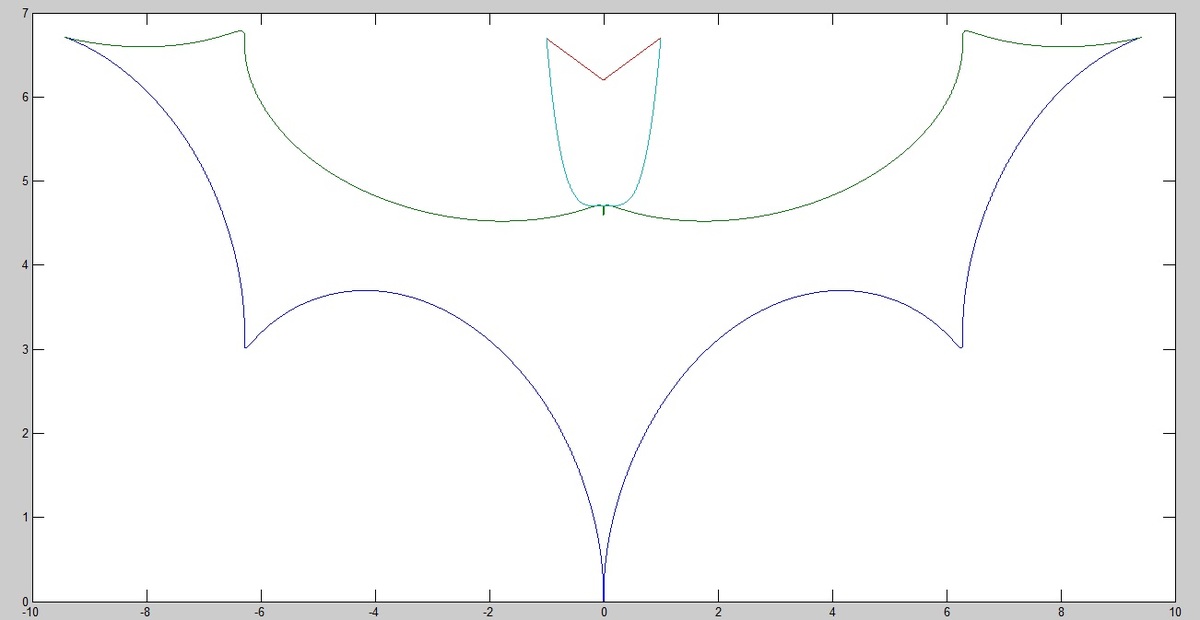
You need to put a lvl cause it gives only 10 points xD it took me some minutes to solve it.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Yeah but you could easily graph it, no sense in free points...

Hobart Pao - 5 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...