Spring 26-09-2020
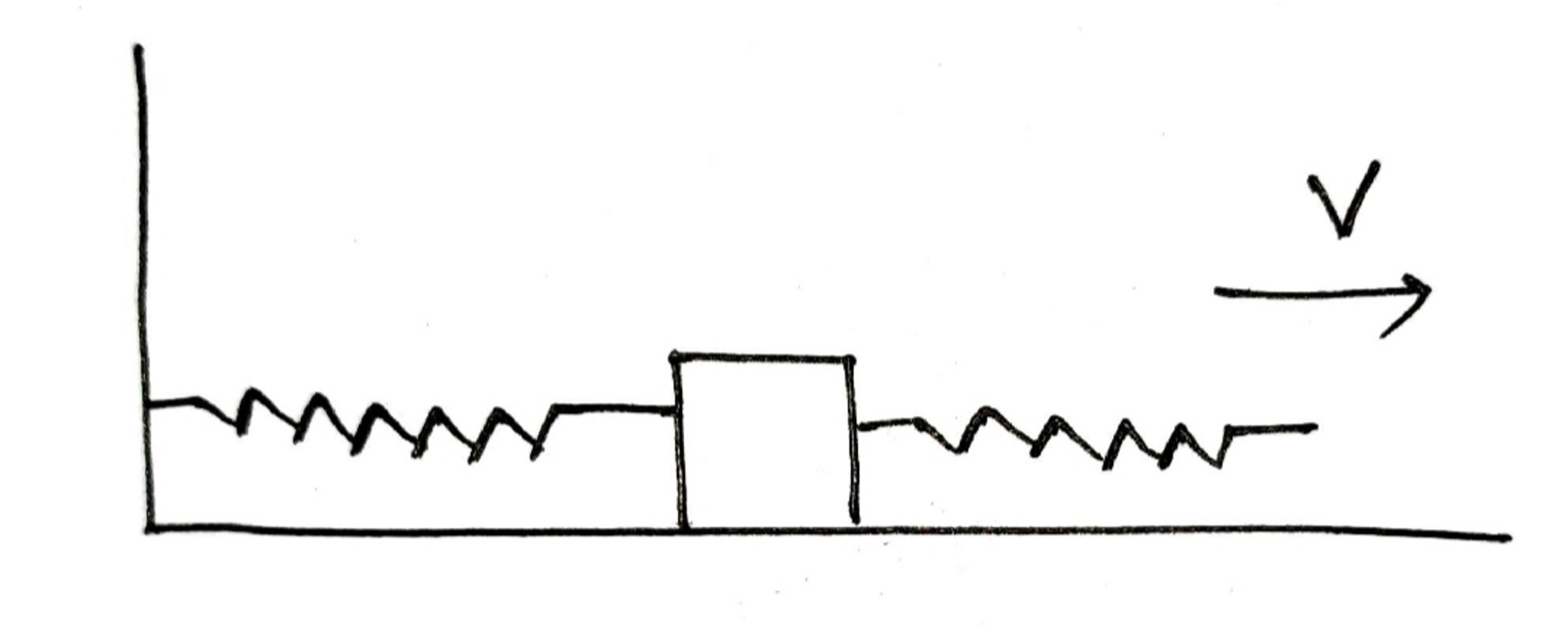 A block of mass
placed on a frictionless horizontal floor is connected with two identical springs each of force constant
.
A block of mass
placed on a frictionless horizontal floor is connected with two identical springs each of force constant
.
One end of the left
spring is connected to a fixed support and one end of the right spring is free. Initially the block is at rest, the springs are collinear and relaxed.
If someone begins to pull the free end of the right spring with a constant velocity
away from the wall, how far will the block move before it acquires a speed of
.
Answer comes in the form of
Type
The answer is 1.110.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice problem. Let the left end of the left spring be fixed at the origin. The X coordinate of the mass is x 1 and the X coordinate of the rightmost point of the right spring is x 2 . Say both springs have a natural length of L o . We know that:
x ˙ 2 = v x 2 ( 0 ) = 2 L o
⟹ x 2 = v t + 2 L o
Now, the kinetic energy of the system is:
T = 2 m x ˙ 1 2 V = 2 k ( ( x 2 − x 1 − L o ) 2 + ( x 1 − L o ) 2 )
Plugging in the expression for x 2 and substituting x = x 1 − L o gives:
T = 2 m x ˙ 2 V = 2 k ( ( v t − x ) 2 + x 2 )
x ( 0 ) = x ˙ ( 0 ) = 0
Now, Lagrangian Mechanics can conveniently handle the rest. I am leaving out this step and presenting the equation of motion, which can also be easily derived using Newton's law (The reader may try this by him/her self):
m x ¨ + 2 k x = k v t x ( 0 ) = x ˙ ( 0 ) = 0
The solution of this equation is (again, I have left out the steps):
x = 2 v ( t − ω sin ( ω t ) ) ω 2 = m 2 k
Now,
x ˙ = 2 v ( 1 − cos ( ω t ) )
x ˙ = v only when cos ( ω t ) = − 1 . Therefore:
t = ω π
Plugging this into the solution for x gives:
x = 2 ω v π x = ( 2 2 π ) v k m ∴ α = 2 2 π