Ball and Spring mechanics

Classical Mechanics Level 2

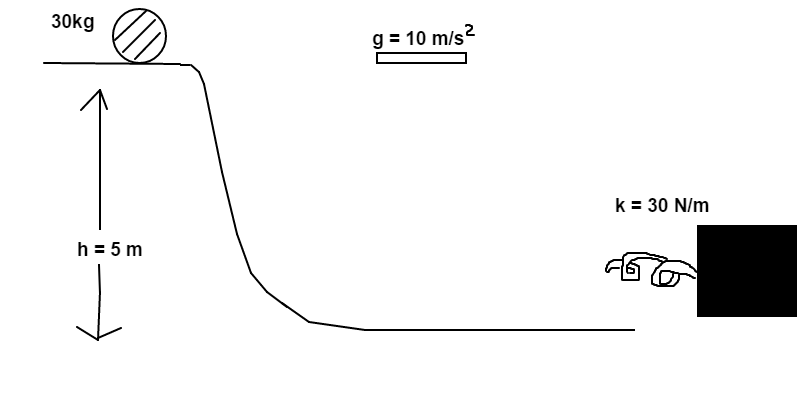
A ball with a mass ( m m ) of 30 kg 30\text{ kg} , is placed on top of a frictionless hill at a height ( h h ) of 5 m 5\text{ m} . How much will the spring at the bottom of the hill be displaced in order to stop the ball if the spring constant ( k k ) is 30 N m 30 \frac{N}{m} ?

Note : A s s u m e g = 10 m s 2 U s p r i n g = 1 2 k x 2 U p o t e n t i a l = m g h Assume \space g = 10 \frac{m}{s^2} \\ U_{spring} = \frac{1}{2} k x^2 \\ U_{potential} = mgh

20 m 20\text{ m} 5 m 5\text{ m} 15 m 15\text{ m} 10 m 10\text{ m}

David Hontz by David Hontz , 26, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Hontz
Jun 9, 2016

All the potential energy of the ball at the top of the hill will be transferred to the spring; therefore, U p o t e n t i a l = U s p r i n g m g h = 1 2 k x 2 x = 2 m g h k = 2 ( 30 k g ) ( 10 m s 2 ) ( 5 m ) 30 N m = 100 = 10 m U_{potential} = U_{spring} \\ mgh = \frac{1}{2} k x^2 \\ x = \sqrt{\frac{2mgh}{k}} = \sqrt{\frac{2(30kg)(10 \frac{m}{s^2})(5m)}{30\frac{N}{m}}} = \sqrt{100} = \boxed{10m}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...