Spring Compressed on Parabola (Part 2)
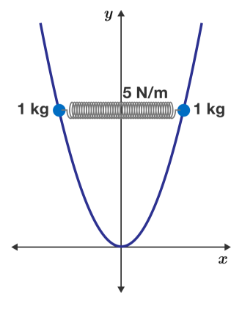
Two beads are at the ends of a spring located on a smooth parabolic wire The spring has a natural length of and a force constant of
The masses are initially held at rest at . They are then released at time .
At what time does the mass / spring system return to its starting location?
Note: The spring is horizontal and gravity is in the direction.
The answer is 1.215.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Spatial coordinates and time derivatives:
x = x y = x 2 x ˙ = x ˙ y ˙ = 2 x x ˙
Kinetic energy (for two masses):
E = 2 2 1 m v 2 = m ( x ˙ 2 + 4 x 2 x ˙ 2 ) = m x ˙ 2 ( 1 + 4 x 2 )
Spring potential energy:
U S = 2 1 k ( 2 x − ℓ 0 ) 2
Gravitational potential energy:
U G = 2 m g x 2
Lagrangian:
L = E − U S − U G = m x ˙ 2 ( 1 + 4 x 2 ) − 2 1 k ( 2 x − ℓ 0 ) 2 − 2 m g x 2
Equation of motion:
d t d ∂ x ˙ ∂ L = ∂ x ∂ L
Evaluation:
∂ x ˙ ∂ L = 2 m x ˙ ( 1 + 4 x 2 ) d t d ∂ x ˙ ∂ L = 2 m [ 8 x x ˙ 2 + x ¨ ( 1 + 4 x 2 ) ] ∂ x ∂ L = 8 m x x ˙ 2 − 2 k ( 2 x − ℓ 0 ) − 4 m g x
Left / right equivalence:
2 m [ 8 x x ˙ 2 + x ¨ ( 1 + 4 x 2 ) ] = 8 m x x ˙ 2 − 2 k ( 2 x − ℓ 0 ) − 4 m g x 8 x x ˙ 2 + x ¨ ( 1 + 4 x 2 ) = 4 x x ˙ 2 − m k ( 2 x − ℓ 0 ) − 2 g x x ¨ ( 1 + 4 x 2 ) = − 4 x x ˙ 2 − m k ( 2 x − ℓ 0 ) − 2 g x
Second derivative of x:
x ¨ = 1 + 4 x 2 − 4 x x ˙ 2 − m k ( 2 x − ℓ 0 ) − 2 g x
Numerical integration, starting from appropriate initial conditions, yields a return time of t ≈ 1 . 2 1 5