Spring to the top
A heavy mass is attached to a spring of natural length 8 m and spring constant k = 1 0 0 N/m . The top of the spring is attached to a ceiling, which is 1 0 m above the mass. The mass is then pulled horizontally for a distance of 1 0 m and released. It therefore slides back along the ground towards where it started. What is the kinetic energy of the mass in Joules when it returns to its starting point?
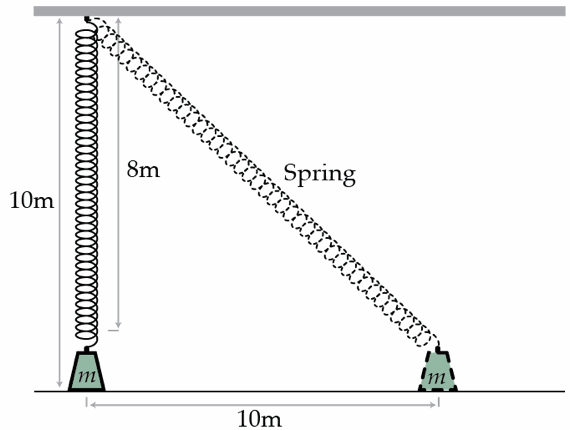
Details and assumptions
- The floor is frictionless.
- The mass is heavy enough that it always rests on the ground.
- Treat the mass as a point mass.
The answer is 1686.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
why the xf should + the height of the point mass? my teacher told me that delta x is only counted from the height of spring only not high of point mass included.
Read the top comments/the top of my explanation, please.
By the Work-Energy Theorem, W = Δ K . Since the initial kinetic energy is 0, the final kinetic energy is simply the change in the kinetic energy, or the work done by the mass on the spring. Since the force within the spring is variable, we must use integration to compute the work: W = ∫ F ⋅ d x . The magnitude of the force exerted by mass on the spring is F = k ( l − 8 ) , where l is the length of the spring (8 is the natural length of the spring. However, since our given values are in terms of x (the horizontal distance from the beginning), we must make the substitution l = x 2 + 1 0 0 . We get F ( x ) = k ( x 2 + 1 0 0 − 8 ) Now we take the integral ∫ x = 0 1 0 F ( x ) ⋅ d x . Recall that when we take the dot product of two vectors, we multiply their magnitudes together with the cosine of the angle between them. The cosine of the angle between the force in the spring and the differential of the horizontal displacement is x 2 + 1 0 0 x , therefore, we can rewrite our integral as W = 1 0 0 ∫ x = 0 1 0 x 2 + 1 0 0 x ( x 2 + 1 0 0 − 8 ) d x (the spring constant k = 1 0 0 , is put in front of the integral for simplicity) This integral evaluates to 1686.2 J, the correct answer.
This is exactly how I solved it.
thanks bro
Can't we split the restoring force to a horizontal and vertical component and then use the horizontal component, i.e, something of the form K*cos(theta) where tan(theta) = 8/10 ?
When the mass is pulled, it has elastic potential energy. When it returns to its starting point, it has elastic potential energy and translational kinetic energy.
By principle of conservation of energy, ∑ E i n i t i a l = ∑ E f i n a l .
2 1 k x i 2 = 2 1 k x f 2 + E k
2 1 ( 1 0 0 ) ( 2 0 0 − 8 ) = 2 1 ( 1 0 0 ) ( 1 0 − 8 ) + E k
E k = 1 6 8 6 . 2 J
Sorry, it's principle of conservation of energy , not principle of conservation of momentum.
By conservation of mechanical energy, K E 1 + P E 1 = K E 2 + P E 2 . K E 1 = 0 , so K E 2 = P E 1 − P E 2 . Doing some trigonometry, we find that the length of the extended spring is 1 0 2 , so the potential energy there is 2 1 ( 1 0 0 ) ( 1 0 2 − 8 ) 2 . Thus the kinetic energy is 2 1 ( 1 0 0 ) ( 1 0 2 − 8 ) 2 − 2 1 ( 1 0 0 ) ( 2 ) 2 = 1 6 8 6 . 2 1 4 J.
When the spring is pulled over a horizontal distance of 10m, its length is 1 0 2 + 1 0 2 = 2 0 0
Its extended length is x= 2 0 0 -8 . Its total potential energy is 2 1 k x 2 =1886.29J
When return to starting point, the spring still has extension of 10-8=2 m and potential energy= 2 1 k( 2 2 )=200J . So when the spring returns to starting point, the portion of potential energy converted to kinetic energy is 1886.29-200= 1 6 8 6 . 2 9 J
(KE+PE)initial = (KE+PE)final by Law of Conservation of Energy 0+ \frac{1}{2}ke {1}^2 = KE + \frac{1}{2}ke {2}^2 \frac{1}{2}(100)(10\sqrt{2} - 8)^2 = KE+ \frac{1}{2}(100)(10-8)^2 KE = 50(2^2)- 50(10\sqrt{2} - 8)^2 = 1686.2 J
This diagram is extremely confusing---I thought it meant that the mass given was simply 2m high (like the previous problem, I thought it was extraneous information). Apart from this, the problem is relatively simple.
By conservation of energy: T 0 ∑ T 0 + V 0 ∑ V 0 = T f ∑ T f + V f ∑ V f Clearly, then, kinetic energy: T 0 = 0 J And potential energy: V 0 = 2 1 k l 2 Where we have: l = x f − x 0 = 1 0 2 − 8 Then: V 0 = 2 1 k ( 1 0 2 − 8 ) 2 At its normal position: V f = 2 1 k ( 2 2 ) This give us: T f = V 0 − V f = 2 1 ( 1 0 0 ) ( 1 0 2 − 8 ) 2 − 2 1 ( 1 0 0 ) ( 2 2 ) ≈ 1 6 8 6 . 2 J Which is our answer.