Spring with Mass
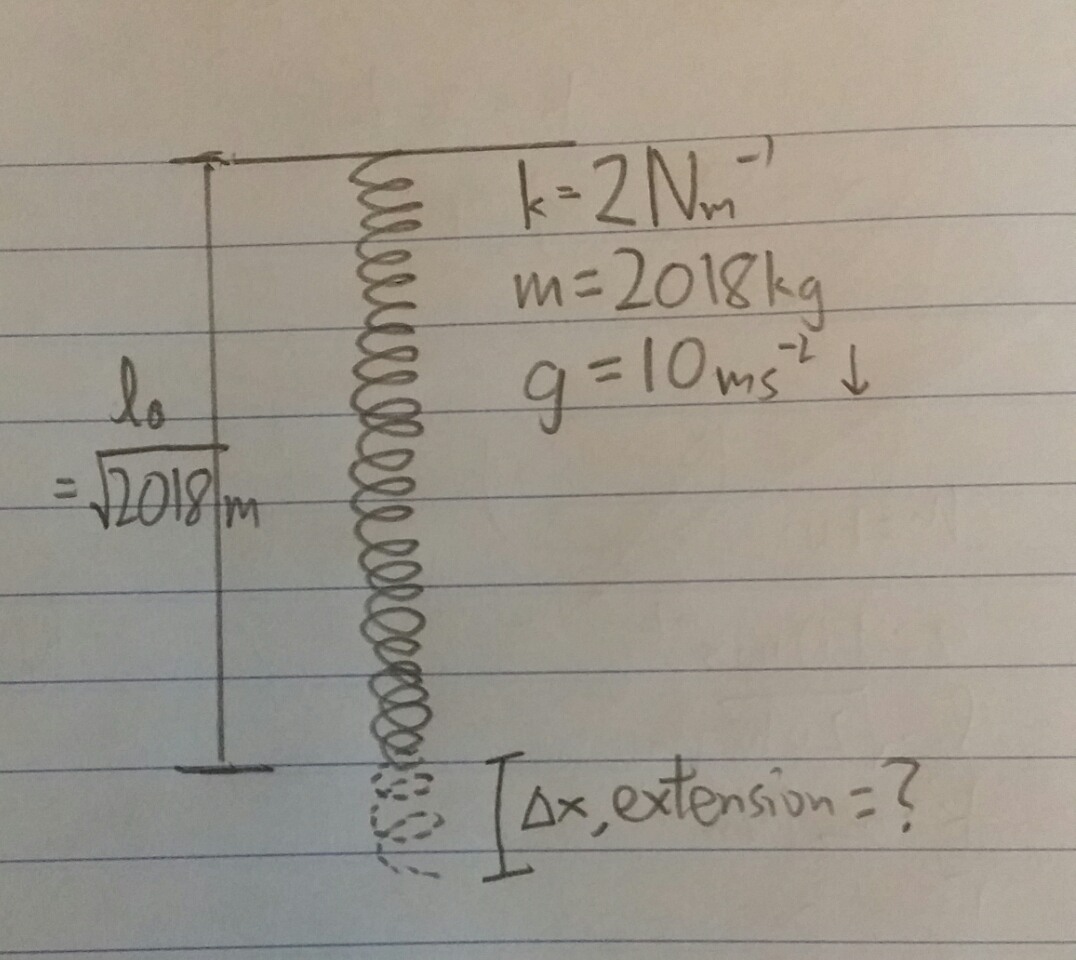 Given an spring with mass,
m
=
2
0
1
8
kg distributed equally. Find its length of extension with details below.
Given an spring with mass,
m
=
2
0
1
8
kg distributed equally. Find its length of extension with details below.
Details and assumption :
M a s s , G r a v i t y , O r i g i n a l l e n g t h , M o d u l u s o f e l a s c i t y , m = 2 0 1 8 k g . g = 1 0 m s − 2 . l 0 = 2 0 1 8 m . k = 2 N m − 1 . The spring doesn't exceed elastic limit.
The answer is 5045.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I don't think the distribution of mass which is assumed to be uniform is correct in the final state of the system, because the lower portions of the spring will be stretched less in comparison to the upper portions and hence if you break the spring into small rings mass won't be distributed uniformly.
The solution to this problem can be determined directly by realizing that the original length of the spring is irrelevant. The spring extension will be 5045m regardless of how long the spring may be with no extending force acting upon it. A spring extension is a function of the force acting on the spring and the spring constant K (modulus of elascity). X=-F/K.
Note that this is a linear expression. The extension displacement varies directly with the force.
In this problem it is given that the springs mass is distributed equally. Consider the spring under no loading force Gravity = to 0.0 m/s^2. Consider any location along the length of the spring. If gravity is not 0 any part of the spring below this location would contribute to the force on the spring at this location. The spring elongation force at any location could be calculated using F=ma. Where mass is the mass of the spring below the location and a is gravity. It will not make any difference where in space this location on the spring ends up after the spring is extended. The extension of the spring above the location has no effect on the force that gravity is exerting on the mass below the location on the spring.
Suppose the length of the original spring was marked with an infinite number divisions. As the spring is stretched these marks will move downward in space but remain at the same location on the spring's surface. Since the distribution of mass along the spring (between divisions) is constant then the resulting force down the length of the spring will also decrease linearly when a gravitation force is applied. At the top end, the force will be a result of the entire mass of the spring hanging from that location . The force will uniformly decreasing to a force approaching 0 at the lower end of the spring. If the rate of change of the stretching force in uniform and linear then the mean force can be determined and applied to the spring extension calculation. i.e. The upper portion of the spring will be experiencing more force then the lower portion but the overall average force along the entire length of the spring can be easily calculated.
F m e a n = 2 F t o p + F B o t t u m = 2 0 + 2 0 1 8 ∗ 1 0 = 1 0 0 9 0 n
X e x t e n t i o n = K F m e a n = 2 1 0 0 9 0 = 5 0 4 5 m
Break the whole spring into t small springs, or think the spring as the combine of t small springs together. ( t is a very very large number). Obviously, their(the small spring) mass, m = t 2 0 1 8 , length, l = t 2 0 1 8 , modulus k = 2 t .
Now, the i -th small spring which count from down is exerted by force, F i = ( j = 0 ∑ i − 1 m j ) g = 2 0 1 8 0 t ( i − 1 ) The extension of the i -th small spring is x i = k F i = 1 0 0 9 0 t 2 ( i − 1 ) . The whole extension is = = = = j = 0 ∑ t x j t 2 1 0 0 9 0 ( j = 0 ∑ t ( i − 1 ) ) t 2 1 0 0 9 0 × 2 ( t − 1 ) t t 5 0 4 5 ( t − 1 ) 5 0 4 5 The bigger the t , t t − 1 converge to 1 . Hence, the answer is 5 0 4 5 .