Springs Supporting Hanging Mass

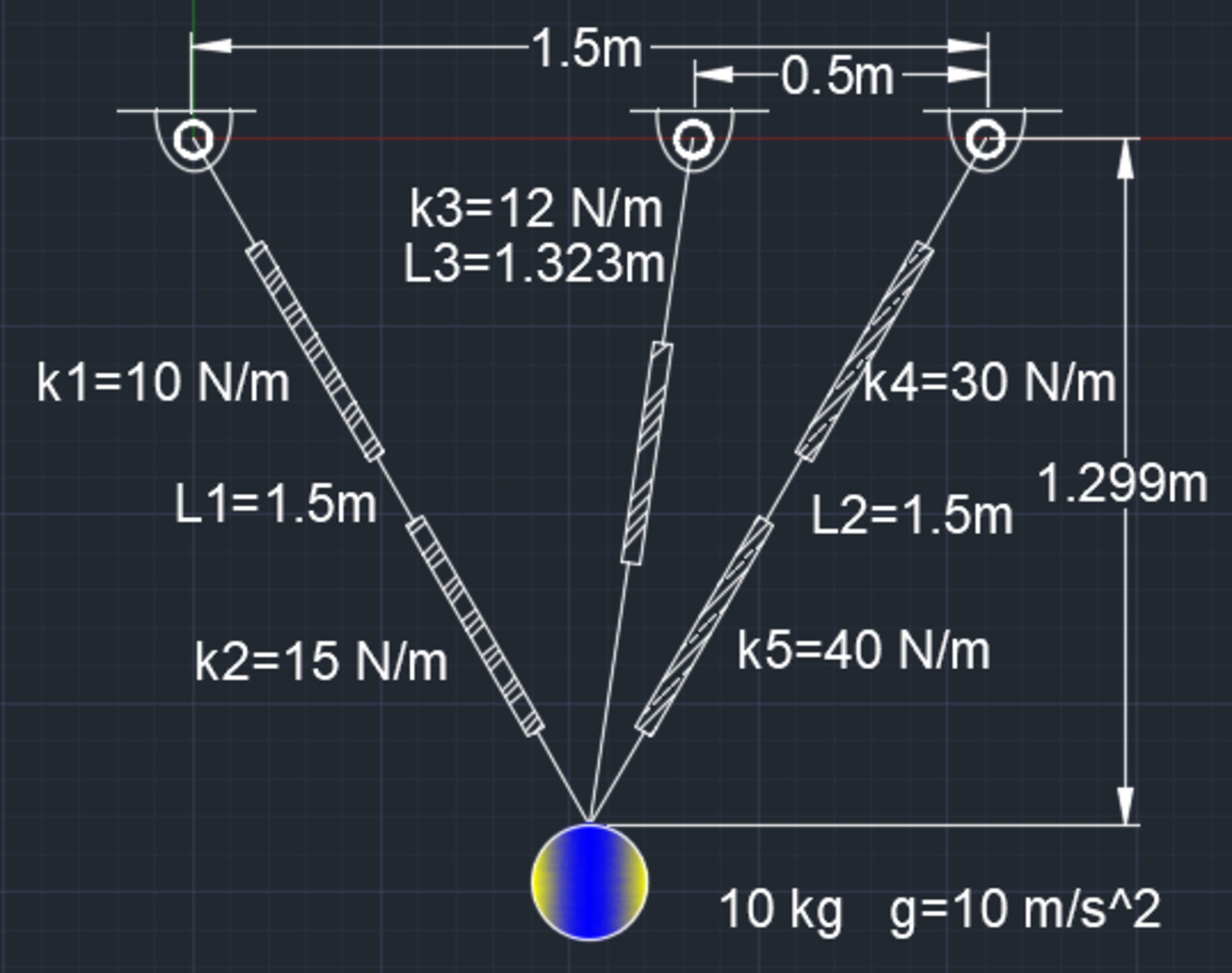Classical Mechanics Level pending

Five springs support a 10 kg mass as indicated in the diagram. The spring constants and unstretched lengths are given. What is the distance of the mass from the leftmost support in the equilibrium condition? Give your answer in meters to the nearest 1/100 th. Note: The value 1.299 is the initial distance before the mass is released.


The answer is 4.41.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
Mar 15, 2020

Nice problem. I used a hill-climbing algorithm to solve. I reworked the nomenclature a little bit to suit my taste. Results are commented at the bottom of the code. I would suggest removing the 1.299 1.299 meter vertical distance measurement from the picture, as it is somewhat misleading. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
 
import math
import random

# Simulation params

x1 = 0.0
y1 = 0.0

x2 = 1.0
y2 = 0.0

x3 = 1.5
y3 = 0.0

L1 = 1.5
L2 = 1.323
L3 = 1.5

k1 = 10.0*15.0/(10.0+15.0)
k2 = 12.0
k3 = 30.0*40.0/(30.0+40.0)

m = 10.0
g = 10.0

####################################################

delta = 0.001

####################################################

x = 1.5 * random.random()
y = -5.0 * random.random()

Fmin = 9999999.0

for j in range(0,10**6):

    xm = x + delta*(-1.0 + 2.0*random.random())   # mutated params
    ym = y + delta*(-1.0 + 2.0*random.random())

    v1x = x1 - xm   # vectors from mass to spring anchor points
    v1y = y1 - ym

    v2x = x2 - xm
    v2y = y2 - ym

    v3x = x3 - xm
    v3y = y3 - ym

    v1 = math.hypot(v1x,v1y)   # stretched spring lengths
    v2 = math.hypot(v2x,v2y)
    v3 = math.hypot(v3x,v3y)

    u1x = v1x/v1                # unit vectors along springs
    u1y = v1y/v1

    u2x = v2x/v2
    u2y = v2y/v2

    u3x = v3x/v3
    u3y = v3y/v3

    s1 = v1 - L1               # spring stretches
    s2 = v2 - L2
    s3 = v3 - L3

    F1s = k1*s1                # spring force magnitudes
    F2s = k2*s2
    F3s = k3*s3

    F1sx = F1s * u1x           # spring force vectors
    F1sy = F1s * u1y

    F2sx = F2s * u2x
    F2sy = F2s * u2y

    F3sx = F3s * u3x
    F3sy = F3s * u3y

    Fgx = 0.0                  # gravity force vector
    Fgy = -m*g

    Fx = F1sx + F2sx + F3sx + Fgx     # net force vector
    Fy = F1sy + F2sy + F3sy + Fgy

    F = math.hypot(Fx,Fy)      # net force magnitude

    if F < Fmin:                # accept mutation if Fmin decreases

        Fmin = F

        x = xm
        y = ym

####################################################

print Fmin
print ""
print x
print y
print math.hypot(x,y)

#3.60779638463e-05

#1.06927858381
#-4.27368413773
#4.40542084242

2 Helpful 2 Interesting 2 Brilliant 0 Confused

I guess I'll add a note to clarify that it is the initial depth. Thanks!

A Former Brilliant Member - 1 year, 2 months ago

1 Helpful 2 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...