Sprinkler Dome

Calculus Level 3

Grass grows on the floor inside a hemispherical dome. In the centre of the dome is a sprinkler, which projects water from ground level in all directions, with an angle of inclination from the horizontal that varies from 0 to 90 degrees.

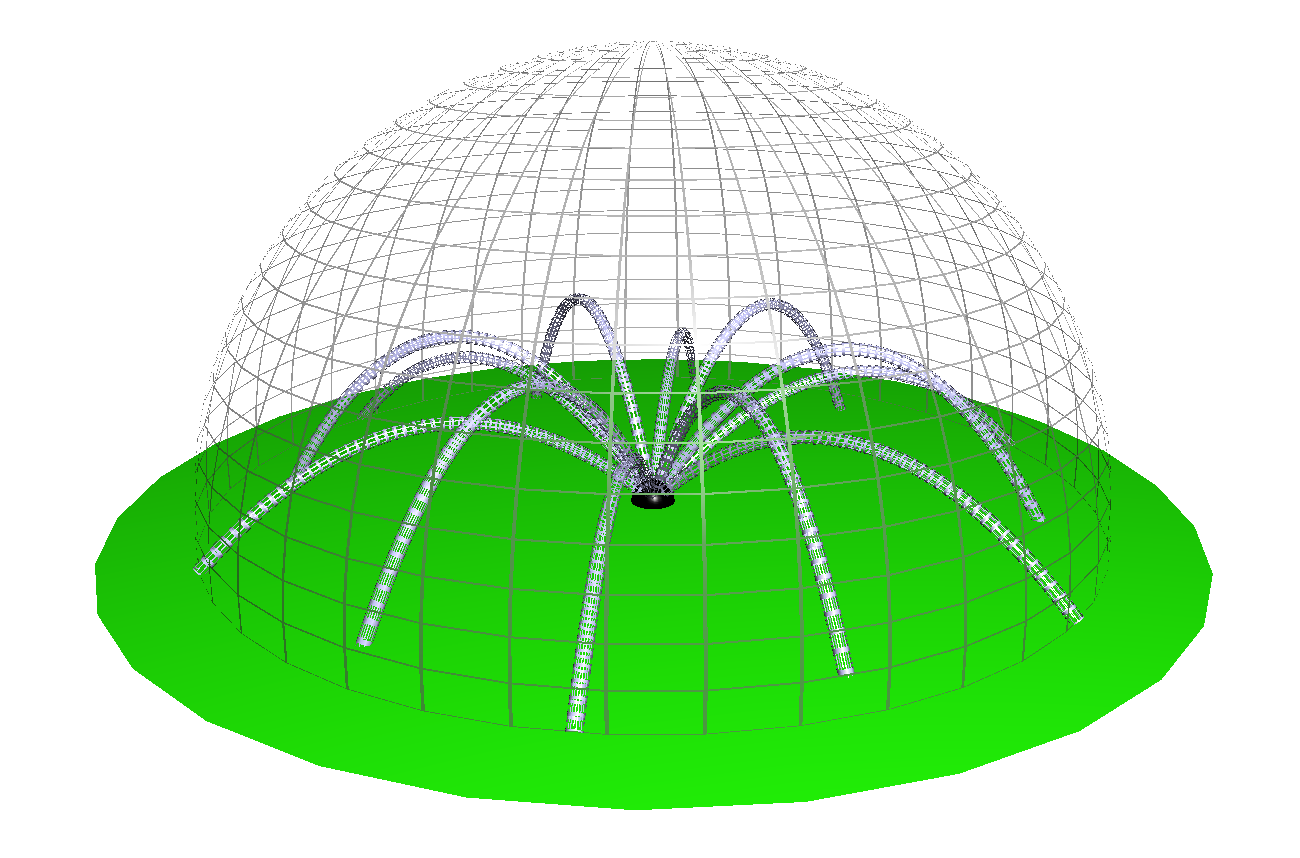
The velocity of the water as it leaves the sprinkler is constant, and just enough that the sprinkler can reach the grass at the edge of the dome at its maximum range.

The fraction of the volume of the hemisphere that the water in the sprinkler can reach can be expressed in the form $\frac ab$ , where $a$ and $b$ are coprime positive integers. Find $a+b$ .

The answer is 11.

2 solutions

Otto Bretscher
Oct 29, 2018

We know from introductory physics that the horizontal range of a projectile is twice the vertical range and that the envelope of all trajectories is a paraboloid. Thus the volume of the hemisphere is $\frac{2}{3}\pi r^3$ and the volume of the paraboloid is $\frac{1}{4}\pi r^3$ , half the volume of the circumscribed cylinder. The ratio is $\frac{3}{8}$ and the answer is $\boxed{11}$ .

Aaghaz Mahajan
Oct 28, 2018

Hint :- Find the envelope of the projectiles.......Then its simple calculation of volume of a paraboloid..........!!

Sprinkler Dome

The answer is 11.

2 solutions

0 pending reports