This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Much better solution than siddhartha
Log in to reply
siddhartha solution is 100% correct
awesome solution
Half of the square root of 2 is .707
Log in to reply
Yes but the square root of 0.5 is .707 as it asked for k
WORNG METHOD
Log in to reply
What? How can you have a wrong method?? The answer is the same!
Half of 2 is 2 2 = ( 2 ) 2 2 = 2 1 = 2 1
Therefore k = 2 1 = 0 . 5
ITS A WROND ... METHOD IS TRUE... BY TAKING SQUARE ROOT ON BOTH SIDE UNDER ROOT CUT FROM SQUARE K = 2 ANSWER
We can write the problem as determining k such that: 2 1 2 = k squaring both sides: ⇒ k = 4 1 ⋅ 2 = 2 1 = 0 . 5
2 1 × 2 = 2 2 = 4 2 = 2 1 so k=0.5
here it is:
√k = √2/2
or, (√k)^2 = (√2/2)^2
or, k = 2/4=1/2=.5
( k ) = 2 2 ⟹ k = 4 2 = 2 1 = 0 . 5
Squaring an evaluation is bad prose.
You can write this;
k = c
k 2 = c 2
But you can't write
k = c
( k = c ) 2
k 2 = c 2
It's mathematical nonsense.
Log in to reply
No "()" indicates an attempt to rationalize numbers as part of a process to rationalize numbers.
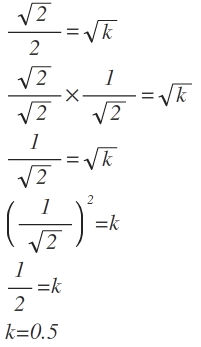
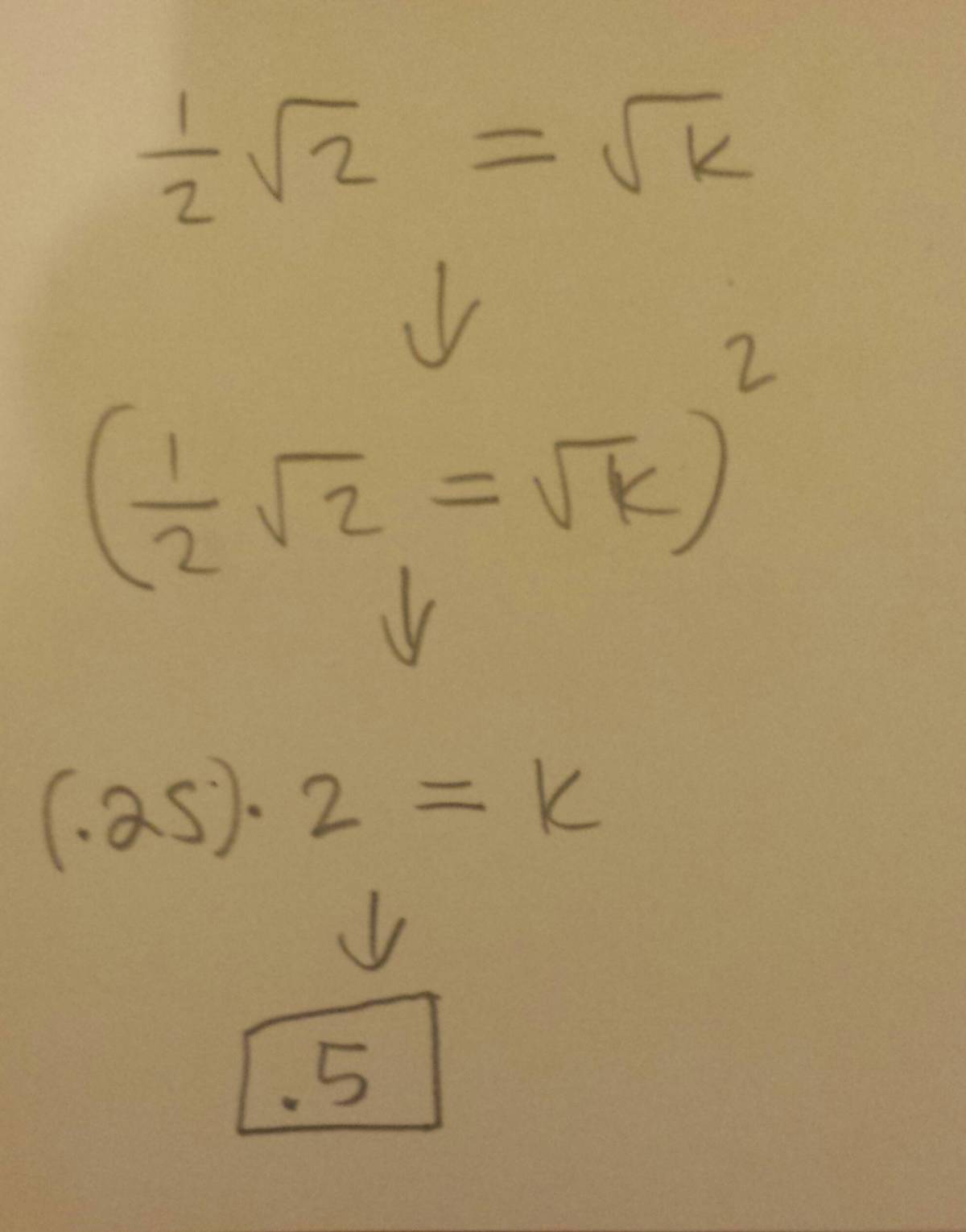
Since the square root of k is half the square root of 2, we can set up an equation like this and solve.
k = 2 2 ( k ) 2 = ( 2 2 ) 2 k = 4 2 = . 5