Square and 2016
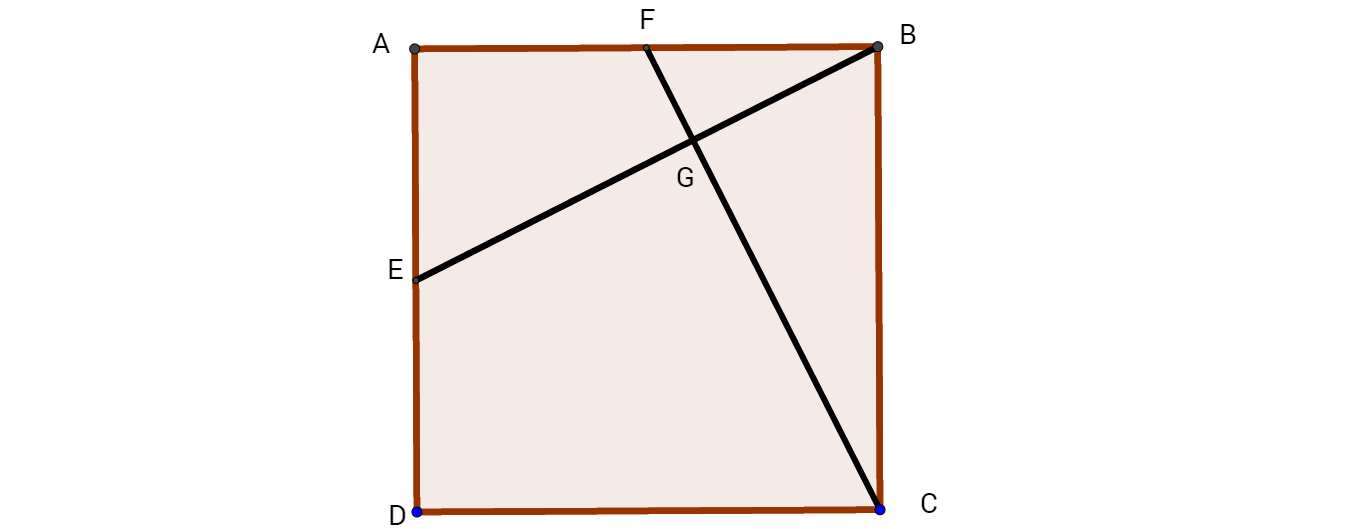
A B C D is a square with side length 2016. E and F are the mid-points of A D and A B respectively. G is the intersection point of C F and B E . Find the length of D G .
The answer is 2016.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
Be careful with the justification of steps. The reason why C D = D C ′ is that E is the midpoint of A D and we have similar triangles / parallel lines.
The mere fact that ∠ C G C ′ = 9 0 ∘ , does not justify that D is the center of the circle. We need the fact that E is the midpoint of A D .
Otherwise, it's a nice construction solution that you have.
Be careful with the justification of steps. The reason why C D = D C ′ is that E is the midpoint of A D and we have similar triangles / parallel lines.
The mere fact that ∠ C G C ′ = 9 0 ∘ , does not justify that D is the center of the circle. We need the fact that E is the midpoint of A D .
Otherwise, it's a nice construction solution that you have.
Again a very very nice solution. Up voted.
Let D = (0,0). Then E =(0,1008), A = (0, 2016), F = (1008, 2016), B = (2016,2016), C = (2016, 0).
Slope of EB = (2016-1008)/(2016-0) = 0.5 y intercept = 1008 so equation of EB is y = 0.5x + 1008
Slope of FC = (2016 - 0)/(1008-2016) = -2. Use that fact to determine that y intercept is 4032. so equation of FC is y = -2x + 4032.
Solving equations determines intersection to be (1209.6, 1612.8).
Use distance formula to find distance DG = sqrt(1209.6 ^2 + 1612.8^2) = 2016
Using coordinate geometry ; makes it a 3 min. Ques. However I liked the ques. & ur sol. +1
The distance formula in the last step can be avoided because it's a 3, 4, 5 right triangle times 2016/5
After Ahmad Saad's solution did not feel like posting my. However as a Varity the sketches present a solution based on similar triangles.

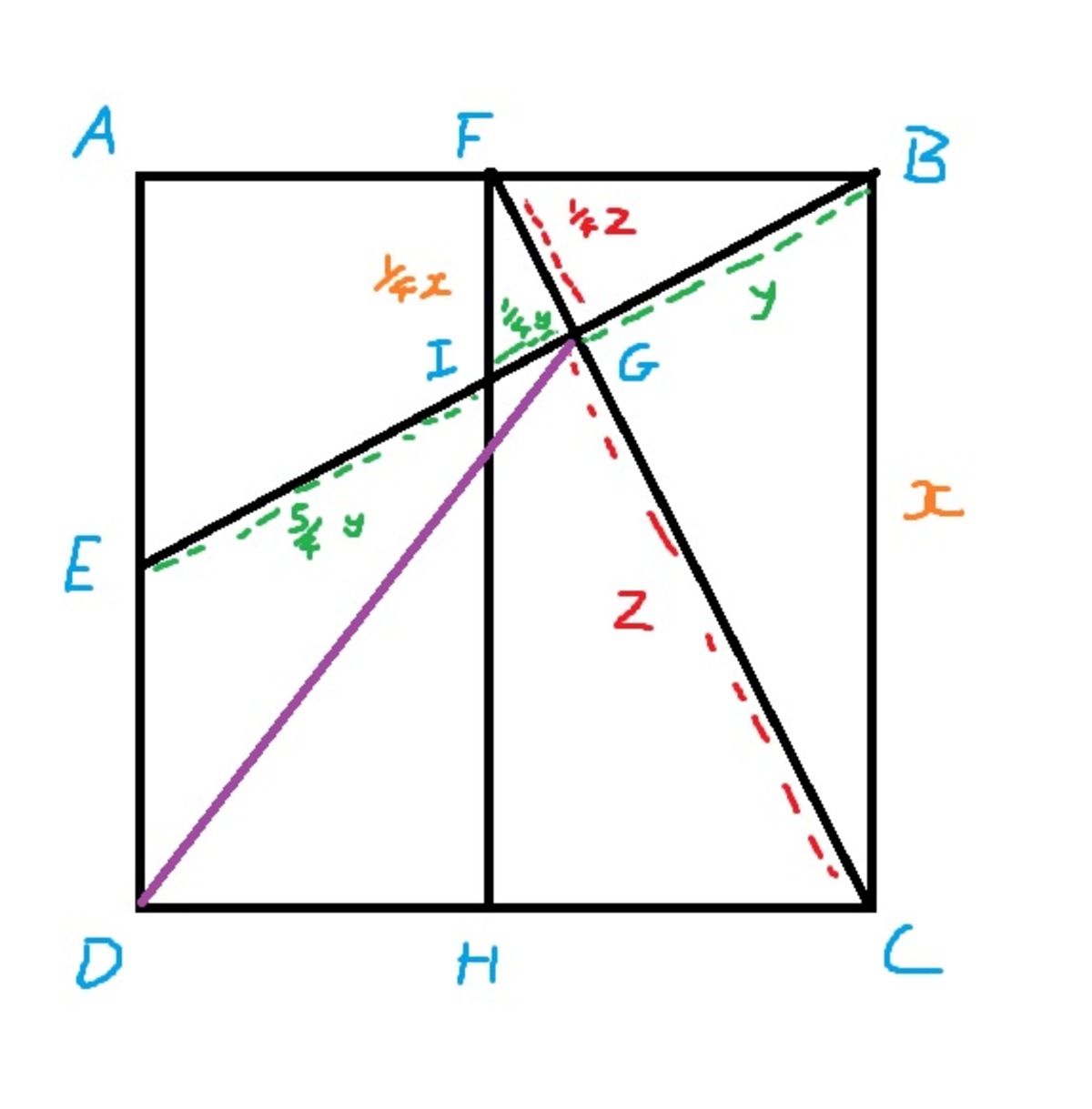 Consider a line going straight down from
F
which cuts the square into 2 halves and cuts
B
E
at
I
. By alternate angles of paraell lines, we have
∠
H
F
C
=
∠
F
C
B
,
∠
F
I
B
=
∠
I
B
C
and by opposite angles,
∠
F
G
I
=
∠
B
G
C
. Triangles
B
G
C
and
F
I
G
have the same angles so they are similar.
Consider a line going straight down from
F
which cuts the square into 2 halves and cuts
B
E
at
I
. By alternate angles of paraell lines, we have
∠
H
F
C
=
∠
F
C
B
,
∠
F
I
B
=
∠
I
B
C
and by opposite angles,
∠
F
G
I
=
∠
B
G
C
. Triangles
B
G
C
and
F
I
G
have the same angles so they are similar.
Let a side of the square have length x Since A B = 2 F B then by similar triangles 2 F I = A E = 2 1 A D = 2 1 x so F I = 4 1 x which implies the triangle F I G is 4 1 scale of triangle F B C . Thereore G C = 4 F G and B G = 4 G I . Let B G = y and C G = z .
Consider the vertical part of z . Since 4 1 z + z = x , we get that z = 5 4 x . Similarly consider the horizontal part of y, E I = B I = y + 4 1 y = 4 5 y by similar triangles from earlier. Then 4 5 y + 4 1 y + y = x ⟹ y = 5 2 x . That means the horizontal part of E G = 4 6 y = 5 3 x .
Finally, we use Pythagoras Theorem on D G . The line has a width 5 3 x horizontally and a height 5 4 x vertically which gives us D G = ( 5 3 x ) 2 + ( 5 4 x ) 2 = x .
Applying this to the question, since the length of the side is 2016 then the length of D G is also 2016.
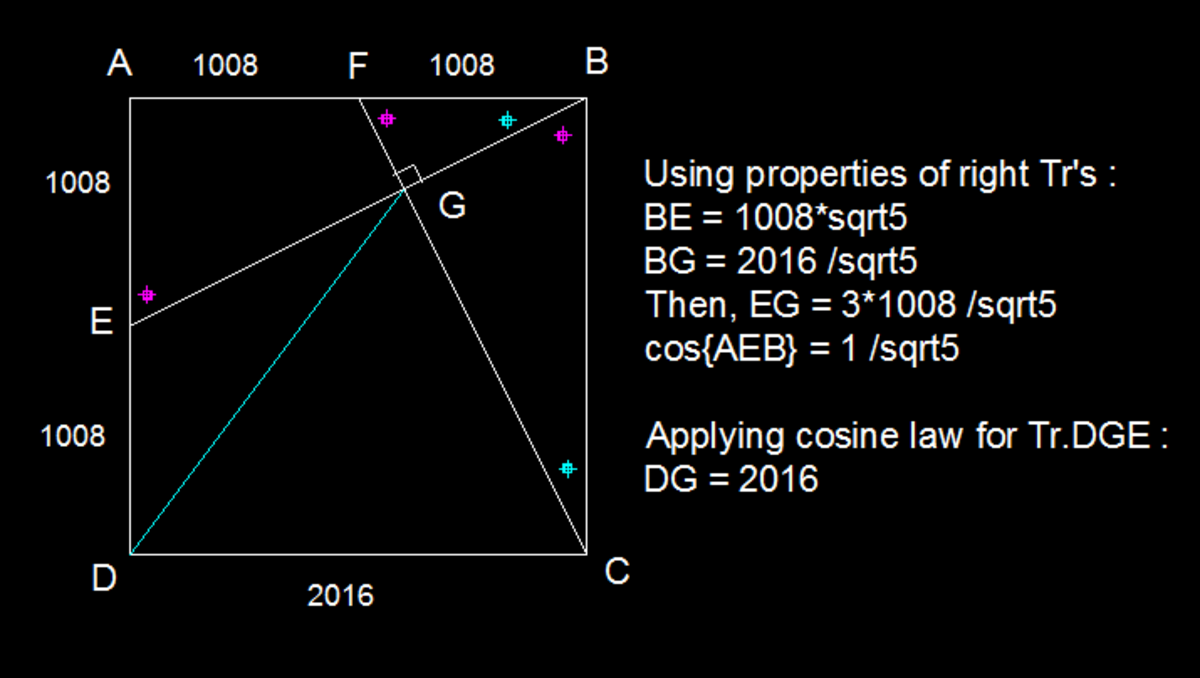
Note that C F and B E are perpendicular. Extend B E and C D to meet at C ′ . Since ∠ C G C ′ = 9 0 ∘ , segment C C ′ = 4 0 3 2 would be the diameter of a circle centered at D , and G would be a point on the circle. Thus, D A = D G = D C = 2 0 1 6 .