Square and a Point
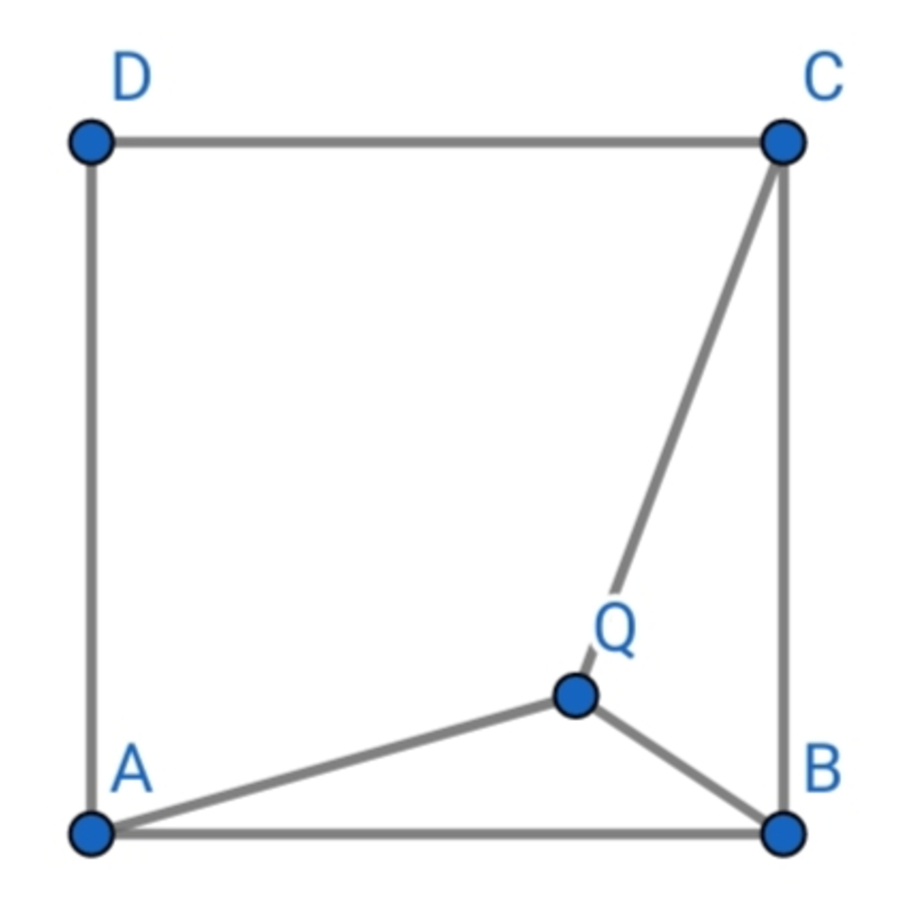
Point Q inside square A B C D is such that A Q = 1 5 9 , B Q = 3 9 , and C Q = 2 1 9 . If the largest possible side length of square A B C D is 4 k , find k − 2 0 2 0 .
The answer is 87980.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the center of square A B C D be the origin O ( 0 , 0 ) of the x y -plane, its side length be 2 a and Q ( x , y ) . Then A ( − a , − a ) , B ( a , − a ) , C ( a , a ) , and D ( − a , a ) and by Pythagorean theorem :
⎩ ⎪ ⎨ ⎪ ⎧ ( x + a ) 2 + ( y + a ) 2 = 1 5 9 ( x − a ) 2 + ( y + a ) 2 = 3 9 ( x − a ) 2 + ( y − a ) 2 = 2 1 9 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
Then ( 1 ) − ( 2 ) : ⟹ 4 a x = 1 2 0 ⟹ a x = 3 0 and ( 2 ) − ( 3 ) : ⟹ 4 a y = − 1 8 0 ⟹ a y = − 4 5 and
( 1 ) : x 2 + 2 a x + a 2 + y 2 + 2 a y + a 2 x 2 + 6 0 + a 2 + y 2 − 9 0 + a 2 x 2 + y 2 + 2 a 2 a 2 x 2 + a 2 y 2 + 2 a 4 3 0 2 + ( − 4 5 ) 2 + 2 a 4 2 a 4 − 1 8 9 a 2 + 2 9 2 5 ( 2 a 2 − 3 9 ) ( a 2 − 7 5 ) ⟹ a = 1 5 9 = 1 5 9 = 1 8 9 = 1 8 9 a 2 = 1 8 9 a 2 = 0 = 0 = 7 5 Multiply both sides by a 2 Taking the larger a
Therefore the largest side length of square A B C D , 2 a = 2 7 5 = 3 0 0 = 4 9 0 0 0 0 ⟹ k − 2 0 2 0 = 9 0 0 0 0 − 2 0 2 0 = 8 7 9 8 0 .
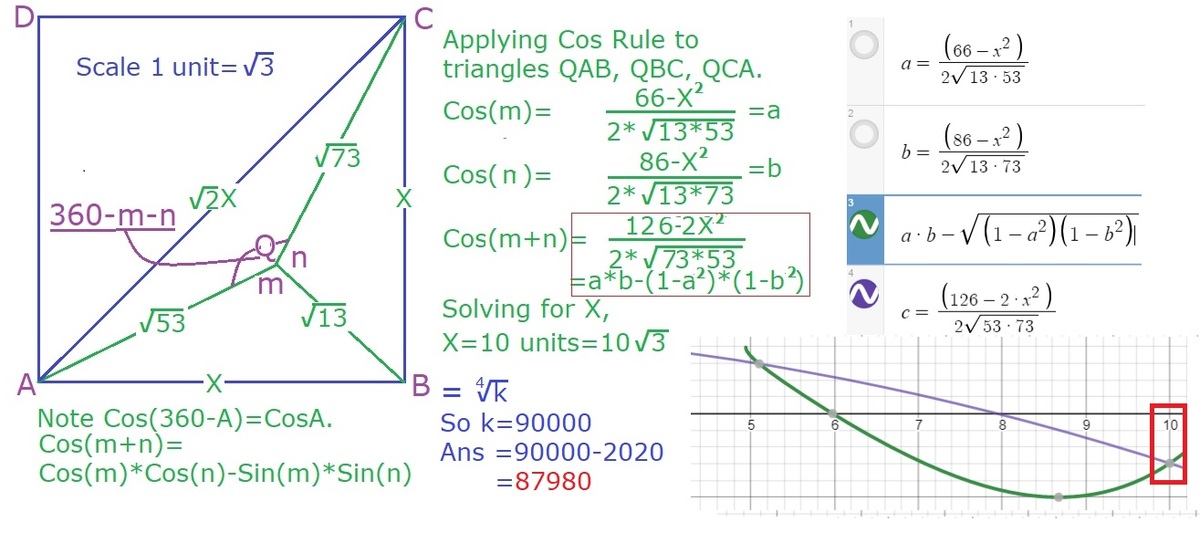
S c a l e 1 u n i t = 3 . 2 ∗ 1 3 ∗ 5 3 6 6 − X 2 ∗ 2 ∗ 1 3 ∗ 7 3 8 6 − X 2 − ( 1 − ( 2 ∗ 1 3 ∗ 5 3 6 6 − X 2 ) 2 ) ∗ ( 1 − ( 2 ∗ 1 3 ∗ 7 3 8 6 − X 2 ) 2 ) = 2 ∗ 5 3 ∗ 7 3 1 2 6 − 2 ∗ X 2 S o 2 6 6 6 . 8 6 − 1 5 2 X 2 + X 4 − ( X 8 − 3 0 4 X 6 + 2 7 9 0 4 X 4 − 7 5 0 4 0 0 X 2 + 5 7 6 0 0 0 0 ) = 1 2 6 − 2 ∗ X 2 ⟹ ( 2 4 0 0 − 1 0 0 X 2 + X 4 ) = X 8 − 3 0 4 X 6 + 2 7 9 0 4 X 4 − 7 5 0 4 0 0 X 2 + 5 7 6 0 0 0 0 ∴ ( 2 4 0 0 − 1 0 0 X 2 + X 4 ) 2 = X 8 − 3 0 4 X 6 + 2 7 9 0 4 X 4 − 7 5 0 4 0 0 X 2 + 5 7 6 0 0 0 0 S o X 8 − 2 0 0 X 6 + 1 4 8 0 0 X 4 − 4 8 0 0 0 0 X 2 + 5 7 6 0 0 0 0 = X 8 − 3 0 4 X 6 + 2 7 9 0 4 X 4 − 7 5 0 4 0 0 X 2 + 5 7 6 0 0 0 0 X 2 = 0 . ⟹ 1 0 4 X 4 − 1 3 1 0 4 X 2 + 2 7 0 4 0 0 = 0 . S o l v i n g q u a d r a t i c i n X 2 , X 2 = 2 6 o r 1 0 0 . P o s s i b l e s o l u t i o n , ( 4 k ) 2 = 1 0 0 , ⟹ k = 1 0 4 u n i t s = ( 1 0 3 ) 4 = 9 0 0 0 0 . S o k − 2 0 2 0 = 8 7 9 8 0 .
Log in to reply
Good use of Desmos software. But you are suppose to use algebra and trigonometry to solve problems here not software.
Log in to reply
Thanks. I am giving the solution you mention.
Coordinate approach: Take B as the origin, let the x -axis run from right to left (or flip the diagram), let the side of the square be s and let the coordinates of Q in this system be ( u , v ) .
Then the information given (using Pythagoras) becomes: u 2 + v 2 ( s − u ) 2 + v 2 u 2 + ( s − v ) 2 = 3 9 = 1 5 9 = 2 1 9
We can eliminate u and v by subtracting the first equation from the second and third in turn: s 2 − 2 s u = 1 2 0 s 2 − 2 s v = 1 8 0 ⇒ u = 2 s s 2 − 1 2 0 ⇒ v = 2 s s 2 − 1 8 0
Now we can substitute back into the first equation to get: 4 s 2 ( s 2 − 1 2 0 ) 2 + ( s 2 − 1 8 0 ) 2 = 3 9
Expanding and tidying up gives s 4 − 3 7 8 s 2 + 2 3 4 0 0 = 0
This is easily solved by treating it as a quadratic in s 2 . The positive roots we get are s = 1 0 3 and s = 7 8 . We're told to take the larger of these, which is the first; the answer is then s 4 − 2 0 2 0 = 8 7 9 8 0 . It's worth noting, though, that the smaller positive value of s places the point Q outside the square A B C D ; there is a unique solution inside the square.
From the figure above, and calling the square side as l , we have:
( 1 ) x 2 + y 2 = 3 9
( 2 ) ( l − x ) 2 + y 2 = l 2 − 2 l x + x 2 + y 2 = 1 5 9
( 3 ) ( l − y ) 2 + x 2 = l 2 − 2 l y + y 2 + x 2 = 2 1 9
Plugging ( 1 ) into ( 2 ) and ( 3 ) :
( 4 ) l 2 − 2 l x = 1 2 0
( 5 ) l 2 − 2 l y = 1 8 0
Making ( 5 ) − ( 4 ) :
2 l x − 2 l y = 6 0
2 l ( x − y ) = 6 0
( 6 ) x = l 3 0 + y
Now substituting ( 6 ) into ( 1 ) :
l 2 9 0 0 + l 6 0 y + y 2 + y 2 = 3 9
Multiplying by l 2 on both sides:
( 7 ) 2 y 2 l 2 + 6 0 l y + 9 0 0 = 3 9 l 2
From ( 5 ) , muliplying by 30 on both sides we can obtain:
( 8 ) 6 0 l y = 3 0 l 2 − 5 4 0 0
And also from ( 5 ) :
2 l y = l 2 − 1 8 0
Squaring:
4 l 2 y 2 = l 4 − 3 6 0 l 2 + 3 2 4 0 0
( 9 ) 2 l 2 y 2 = 2 l 4 − 3 6 0 l 2 + 3 2 4 0 0
Substituting ( 8 ) and ( 9 ) into ( 7 ) :
2 l 4 − 3 6 0 l 2 + 3 2 4 0 0 + 3 0 l 2 − 5 4 0 0 + 9 0 0 = 3 9 l 2
Multiplying by 2 on both sides:
l 4 − 3 6 0 l 2 + 3 2 4 0 0 + 6 0 l 2 − 9 0 0 0 = 7 8 l 2
l 4 − 3 7 8 l 2 + 2 3 4 0 0 = 0
From this, we have:
l 2 = 2 3 7 8 ± 3 7 8 2 − 4 ⋅ 1 4 4 0 0
l 2 = 2 3 7 8 ± 2 2 2
Since we want the larger l :
l 2 = 3 0 0
Since l = 4 k , k = l 4 , so:
k = 9 0 0 0 0 , k − 2 0 2 0 = 8 7 9 8 0