1 Square and 4 Circles in a Triangle

Geometry Level 5

In a right triangle $ABC$ , the height $AD$ to the hypotenuse is drawn. Four congruent circles of radius $r$ are inside the triangle. Two of them are tangent to $AD$ , to one side of the triangle and to each other. Another circle is tangent to two sides of the triangle. The fourth circle is tangent to one side of the triangle and to all three other circles. The smallest square that can be inscribed in triangle $ABD$ has side of length $s$ .

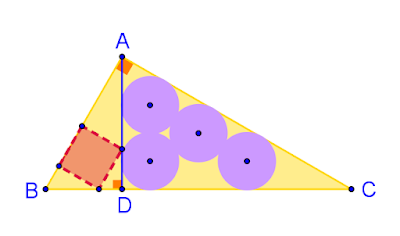Compare the side of the square to the radius of the circles. If their ratio is $\dfrac{s}{r}=\dfrac{\alpha }{\beta }\left( \gamma +\sqrt{\delta } \right)$ , where $\alpha$ , $\beta$ and $\delta$ are prime numbers, submit $\alpha +\beta +\gamma +\delta$ .

$\ \$

Note: A square is inscribed in a triangle when its vertices lay on the sides of the triangle.

The answer is 27.

2 solutions

Nibedan Mukherjee
Aug 7, 2020

To prove MNOP a square inscribed in triangle ABD , have followed the same process as @Thanos Petropoulos .

Thanos Petropoulos
Aug 6, 2020

Denote the centers of the circles by $I_1$ , $I_2$ , $I_3$ , $I_4$ as shown on figure 1. Let $AB=c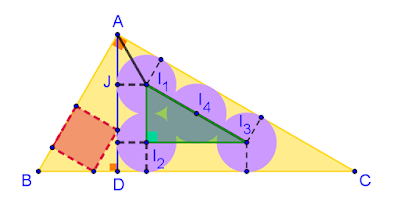$ . figure 1

The sides of $\triangle I_1I_2I_3$ are parallel to the sides of $ADC$ , hence $\triangle I_1I_2I_3$ is right- angled. Since $I_1I_3=4r=2 I_1I_2$ , this triangle is a $30{}^\circ$ - $60{}^\circ$ - $90{}^\circ$ triangle. Consequently, the same holds for $\triangle ADC$ , $\triangle ABC$ and $\triangle ABD$ .

$AD=AJ+JD=r\cot 30{}^\circ +3r=r\left( \sqrt{3}+3 \right)$

$\dfrac{AD}{c}=\sin 60{}^\circ \Rightarrow c=2r\left( \sqrt{3}+1 \right) \ \ \ \ \ {\color{#D61F06}{(1)}}$

In figure 2, we have isolated $\triangle ABD$ , to illustrate a construction of the inscribed square and calculate its side $s$ .

First we construct square $ABHG$ outside $\triangle ABD$ . $DG$ and $DH$ intersect $AB$ at $F$ and $K$ respectively. Lines $LF$ , $MK$ and $DE$ are perpendicular to $AB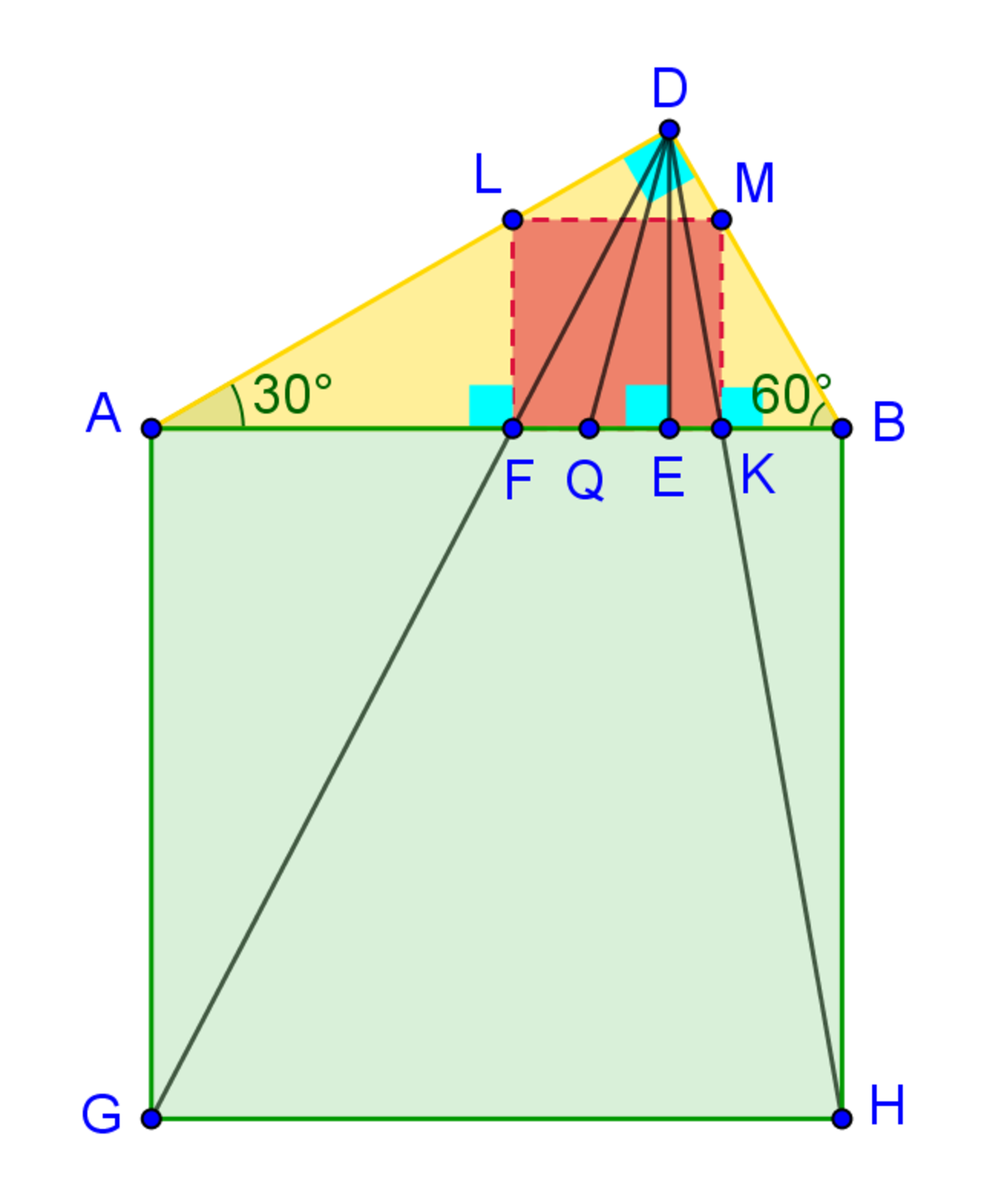$ . figure 2

Due to triangle similarity,

$\dfrac{LF}{AG}=\dfrac{DF}{DG}=\dfrac{FK}{GH}\overset{AG=GH=c}{\mathop{\Rightarrow }}\,LF=FK$ Likewise, $MK=FK$ , thus, $LFKM$ is a square inscribed in $\triangle ABD$ .

Again, taking advantage of triangle similarity,

$\begin{aligned} \dfrac{BK}{KE}=\dfrac{BH}{DE}& \Rightarrow \dfrac{BK}{BK+KE}=\dfrac{c}{c+DE} \\ & \Rightarrow \dfrac{BK}{BD\cdot \cos 60{}^\circ }=\dfrac{c}{c+BD\cdot \sin 60{}^\circ } \\ & \overset{BD=\frac{c}{2}}{\mathop{\Rightarrow }}\,BK=\dfrac{c}{4+\sqrt{3}} \\ \end{aligned}$

Now, for the side of the inscribed square we have

$s=MK=BK\cdot \tan 60{}^\circ =\dfrac{c}{4+\sqrt{3}}\cdot \sqrt{3}\Rightarrow s=c\cdot \dfrac{4\sqrt{3}-3}{13} \ \ \ \ \ {\color{#D61F06}{(2)}}$

${\color{#D61F06}{\left( 1 \right)}},{\color{#D61F06}{\left( 2 \right)}}\Rightarrow s=2r\left( \sqrt{3}+1 \right)\cdot \dfrac{4\sqrt{3}-3}{13}\Rightarrow \dfrac{s}{r}=\dfrac{2}{13}\left( 9+\sqrt{3} \right)$ For the answer, $\alpha =2$ , $\beta =13$ , $\gamma =9$ , $\delta =3$ , hence $\alpha +\beta +\gamma +\delta =\boxed{27}$ .

1 Square and 4 Circles in a Triangle

The answer is 27.

2 solutions

0 pending reports