Square and Sphere - Two Projections
In the x y plane, there is a square with side length 1 , centered on the origin. Each point on the square is projected directly upward ( + z direction) onto the underside of the sphere defined below. Call these projected points ( x ′ , y ′ , z ′ ) .
x 2 + y 2 + ( z − 2 ) 2 = 1
Straight lines are then drawn from the point ( P x , P y , P z ) = ( 0 , 0 , 1 . 5 ) through each point in the set of ( x ′ , y ′ , z ′ ) . The intersection points of these lines with the x y plane form another shape (shown in the image below).
If the area enclosed by the new shape is A , enter ⌊ 1 0 A ⌋ , where ⌊ ⋅ ⌋ denotes the floor function .
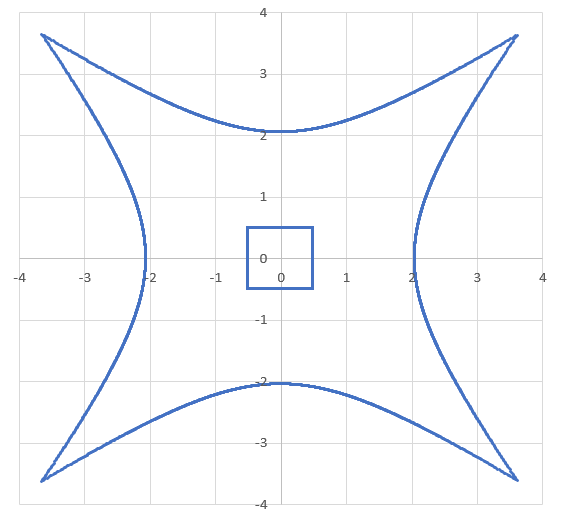
The answer is 245.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The projected points ( x , y , z ) are, for variable y from y = − 2 1 to y = 2 1
( x , y , z ) = ( 2 1 , y 2 , − 1 − x 2 − y 2 )
Then the parametric equation for the line from ( 0 , 0 , 2 3 ) through ( x , y , z ) , with parameter t , is
( x t , y t , 2 3 ( 1 − t ) + z t )
Solving for t where 2 3 ( 1 − t ) + z t = 0 gets us
t = 2 3 ( 1 − 2 y 2 1 + 3 − 4 y 2 )
from which we can derive the cartesian equation for the projected curve on the plane, where X = x t and Y = y t
Y = 4 3 + 4 1 2 7 + 8 X 2
For y = 2 1 , we have x t = y t = 4 3 ( 2 + 2 2 ) , so we integrate for the whole area A
A = 8 ∫ 0 2 3 ( 1 + 2 ) ( 4 3 + 4 1 2 7 + 8 X 2 − X ) d X = 4 9 ( 2 + 2 2 + 3 2 A r c S i n h ( 3 2 + 2 ) )
so that ⌊ 1 0 A ⌋ = 2 4 5
I don't know why but my solution exactly looks like yours! :)
Log in to reply
I copied your solution, that's why
This is a great analytic geometry problem, Steven......deserves every bit to be a Level 5. Thanks very much for posting!
Thanks much. Glad you liked it
I will post a long, detailed solution. First of all, let us consider the curves on the lower part of the sphere formed by the projection points. There will be four curves. Let us consider, first, the curve formed by y ′ = 0 . 5 and x ′ varying from − 0 . 5 to 0 . 5 :
x ′ 2 + 0 . 5 2 + ( z ′ − 2 ) 2 = 1
z ′ 2 − 4 z ′ + 3 . 2 5 + x ′ 2 = 0
z ′ = 2 4 ± 3 − 4 x ′ 2
The expression with the positive square root correspond to the intersection with the upper part of the sphere. The inteserection with the lower part, for y ′ = 0 . 5 (or y ′ = − 0 . 5 , since it will be the same curve only displaced along the y -axis) is, then:
z ′ = 2 4 − 3 − 4 x ′ 2
Likewise, for x ′ = 0 . 5 or x ′ = − 0 . 5 and y ′ varying from − 0 . 5 to 0 . 5 :
z ′ = 2 4 − 3 − 4 y ′ 2
In order to construct the shown curves in the x y plane we have to form a vector from point P = ( P x , P y , P z ) = ( 0 , 0 , 1 . 5 ) to each curve, and then sum point P to this vector multiplyed by some scalar, in order to make the z coordinate equal to 0 . Let us call this vector v and the scalar a :
v = P − ⎣ ⎢ ⎡ x ′ y ′ z ′ ⎦ ⎥ ⎤
For simplicity, since all four curves are symmetric, let us consider the one formed by y ′ = 0 . 5 :
v = ⎣ ⎢ ⎢ ⎡ − x ′ − 0 . 5 1 . 5 − ( 2 4 − 3 − 4 x ′ 2 ) ⎦ ⎥ ⎥ ⎤
So, we want to calculate the extenstion of P along v and then make its z -coordinate equal to 0 :
⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 1 . 5 ⎦ ⎥ ⎤ − a ⋅ ⎣ ⎢ ⎢ ⎡ − x ′ − 0 . 5 1 . 5 − ( 2 4 − 3 − 4 x ′ 2 ) ⎦ ⎥ ⎥ ⎤ .
We then have
x = a x ′ and y = 0 . 5 a , or:
y = x ′ 0 . 5 x .
Making z = 0 , since the curves are on the x y plane:
1 . 5 + 0 . 5 a − a 2 3 − 4 x ′ 2 = 0
a = 3 − 4 x ′ 2 − 1 3
x = 3 − 4 x ′ 2 − 1 3 x ′
x 3 − 4 x ′ 2 = 3 x ′ + x
( 9 + 4 x 2 ) x ′ 2 + ( 6 x ) x ′ − 2 x 2 = 0
x ′ = 2 ( 9 + 4 x 2 ) − 6 x + 1 0 8 x 2 + 3 2 x 4
Since y = x ′ 0 . 5 x :
y = 1 0 8 + 3 2 x 2 − 6 9 + 4 x 2
Which is the upper curve. Likewise, the lower, left and right curve are given by, respectively:
y = − 1 0 8 + 3 2 x 2 − 6 9 + 4 x 2
x = − 1 0 8 + 3 2 y 2 − 6 9 + 4 y 2
x = 1 0 8 + 3 2 y 2 − 6 9 + 4 y 2
To find the vertices, i.e. the intersection of the curves, we have to extend the limit points. Let us consider the upper curve and extend the limit point x ′ = 0 . 5 , i.e.:
⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 1 . 5 ⎦ ⎥ ⎤ − a ⋅ ⎣ ⎢ ⎢ ⎡ − 0 . 5 − 0 . 5 1 . 5 − ( 2 4 − 3 − 4 ⋅ 0 . 5 2 ) ⎦ ⎥ ⎥ ⎤
Making z = 0 :
a = − 3 ( 1 + 2 )
Since x = y = − 0 . 5 a :
x = y = 1 . 5 ( 1 + 2 )
Which are the vertices of the region A , i.e., the intersection of the curves. So, to calculate the area, since it is symmetric, we can consider 8 1 of the total area, the blue area shown in the figure, limited by the upper curve and by y = x , for positive x :
So, A will be 8 times this area:
A = 8 ⎣ ⎡ ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 − 6 9 + 4 x 2 − x ) d x ⎦ ⎤
A = 8 ⎣ ⎡ ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 − 6 9 + 4 x 2 ) d x − 2 x 2 ∣ ∣ ∣ ∣ ∣ 0 1 . 5 ( 1 + 2 ) ⎦ ⎤
A = 8 ⎣ ⎡ ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 − 6 9 + 4 x 2 ) d x ⎦ ⎤ − 9 ( 3 + 2 2 )
Rationalizing the square root on the integral, i.e., multiplying above and below by 1 0 8 + 3 2 x 2 + 6 :
A = 8 ⎣ ⎡ ∫ 0 1 . 5 ( 1 + 2 ) ( 7 2 + 3 2 x 2 [ 9 + 4 x 2 ] ⋅ [ 1 0 8 + 3 2 x 2 + 6 ] ) d x ⎦ ⎤ − 9 ( 3 + 2 2 )
A = 8 ⎣ ⎡ ∫ 0 1 . 5 ( 1 + 2 ) ( 8 ( 9 + 4 x 2 ) [ 9 + 4 x 2 ] ⋅ [ 1 0 8 + 3 2 x 2 + 6 ] ) d x ⎦ ⎤ − 9 ( 3 + 2 2 )
A = ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 + 6 ) d x − 9 ( 3 + 2 )
A = ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 ) d x + 6 x ∣ ∣ ∣ ∣ ∣ 0 1 . 5 ( 1 + 2 ) − 9 ( 3 + 2 2 )
A = ∫ 0 1 . 5 ( 1 + 2 ) ( 1 0 8 + 3 2 x 2 ) d x − 9 ( 2 + 2 )
A = 2 ∫ 0 1 . 5 ( 1 + 2 ) ( 2 7 + 8 x 2 ) d x − 9 ( 2 + 2 )
Make x = 8 2 7 tan ( u ) . Then d x = 8 2 7 sec 2 ( u ) d u . The limits of integration will be 0 and L = tan − 1 [ 2 7 8 ⋅ 1 . 5 ( 1 + 2 ) ] = tan − 1 ( 3 6 + 2 3 ) :
A = 2 8 2 7 ∫ 0 L ( 2 7 + 2 7 tan 2 ( u ) ) sec 2 ( u ) d u − 9 ( 2 + 2 )
A = 5 4 8 1 ∫ 0 L sec 3 ( u ) d u − 9 ( 2 + 2 )
A = 2 2 7 2 ∫ 0 L sec 3 ( u ) d u − 9 ( 2 + 2 )
This integral is a well-known integral and is equal to:
A = 2 2 7 2 ⎣ ⎡ 2 1 [ sec ( u ) tan ( u ) + ln ( sec ( u ) + tan ( u ) ) ] ∣ ∣ ∣ ∣ ∣ 0 L ⎦ ⎤ − 9 ( 2 + 2 )
A = 4 2 7 2 [ sec ( L ) tan ( L ) + ln ( sec ( L ) + tan ( L ) ) ] − 9 ( 2 + 2 )
Where L = tan − 1 [ 3 6 + 2 3 ] . Recalling that if tan ( x ) = k , sec ( x ) = k 2 + 1 :
A = 4 2 7 2 ⎩ ⎪ ⎨ ⎪ ⎧ ⎣ ⎢ ⎡ ( 3 6 + 2 3 ) 2 + 1 ⎦ ⎥ ⎤ ⋅ ( 3 6 + 2 3 ) + ln ⎣ ⎢ ⎡ ( 3 6 + 2 3 ) 2 + 1 + ( 3 6 + 2 3 ) ⎦ ⎥ ⎤ ⎭ ⎪ ⎬ ⎪ ⎫ − 9 ( 2 + 2 )
A = 4 2 7 2 [ ( 3 3 + 2 6 ) ⋅ ( 3 6 + 2 3 ) + ln ( 3 3 + 2 6 + 3 6 + 2 3 ) ] − 9 ( 2 + 2 )
A = 4 2 7 2 [ 3 6 + 5 2 + ln ( 6 + 3 ) ] − 9 ( 2 + 2 )
A = 2 9 + 9 2 + 4 2 7 2 ln ( 6 + 3 ) ≈ 2 4 . 5 2 1 1 5
And thus:
⌊ 1 0 A ⌋ = 2 4 5