Square and Two Circles Problem

Geometry Level 4

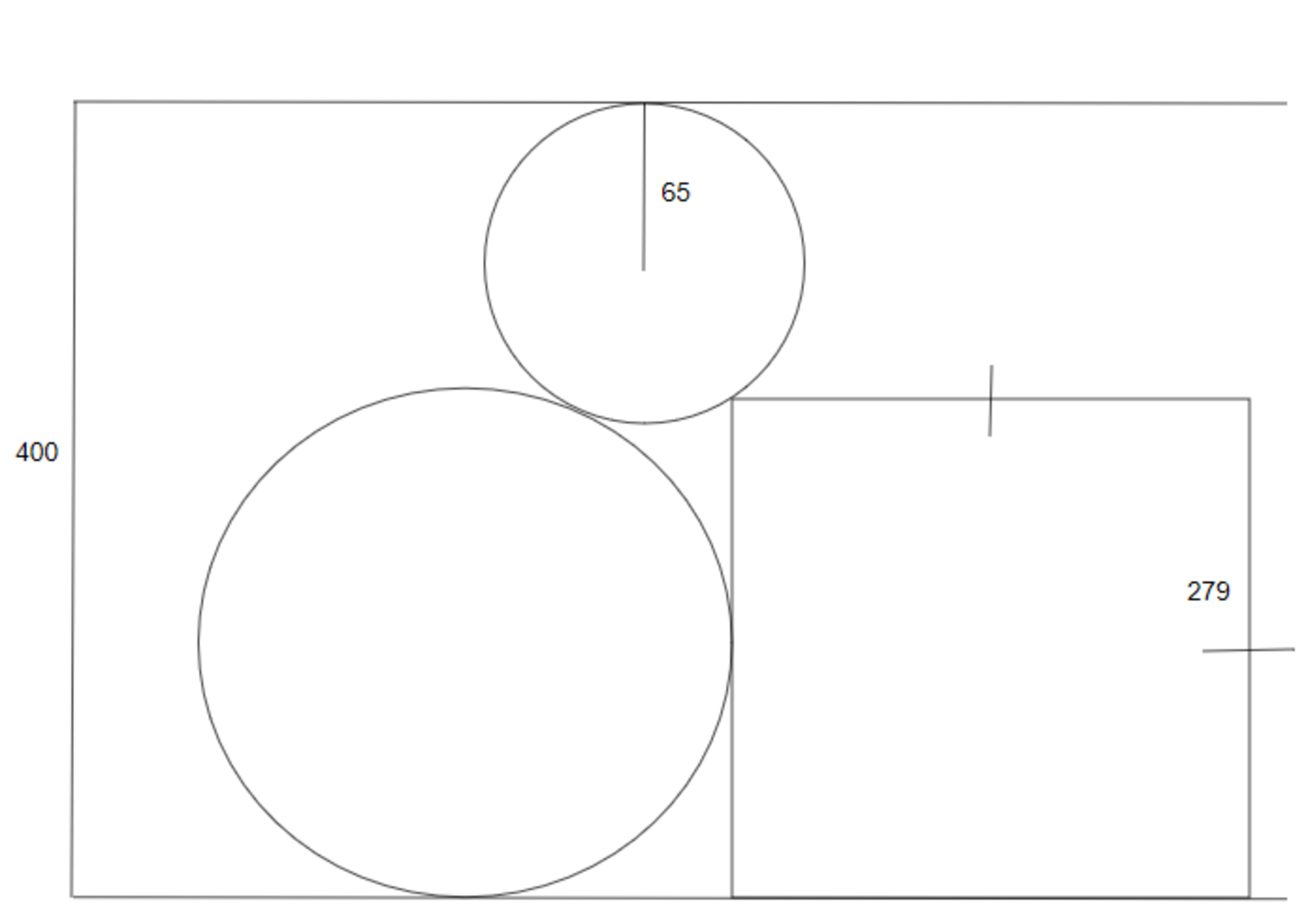
Two circles and a square are tangent to eachother at one point. The height of the whole thing is 400 units, the square has a side length of 279 units, and the small circle has a radius of 65 units. Find the radius of the larger circle to the nearest whole unit.


The answer is 153.

Daniel Araujo by Daniel Araujo , 20, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Let the radius of the large circle be r r . From the figure we note that 65 + ( r + 65 ) 2 − ( r − a ) 2 + r = 400 65 + \sqrt{(r+65)^2-(r-a)^2} + r = 400 , where a = 6 5 2 − b 2 a = \sqrt{65^2 - b^2} . We note that b = 400 − 65 − 279 = 56 b= 400 - 65 - 279 = 56 . ⟹ a = 6 5 2 − 5 6 2 = 33 \implies a = \sqrt{65^2-56^2} = 33 and:

65 + ( r + 65 ) 2 − ( r − a ) 2 + r = 400 ( r + 65 ) 2 − ( r − 33 ) 2 = 335 − r Squaring both sides 196 r + 3136 = r 2 − 670 r + 112225 ⟹ r 2 − 866 r + 109089 = 0 ( r − 713 ) ( r − 153 ) = 0 Since r < 400 ⟹ r = 153 \begin{aligned} 65 + \sqrt{(r+65)^2-(r-a)^2} + r & = 400 \\ \sqrt{(r+65)^2-(r-33)^2} & = 335 - r & \small \color{#3D99F6} \text{Squaring both sides} \\ 196r+3136 & = r^2 -670r + 112225 \\ \implies r^2 -866r + 109089 & = 0 \\ (r-713)(r-153) & = 0 & \small \color{#3D99F6} \text{Since }r < 400 \\ \implies r & = \boxed{153} \end{aligned}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...