Square Business
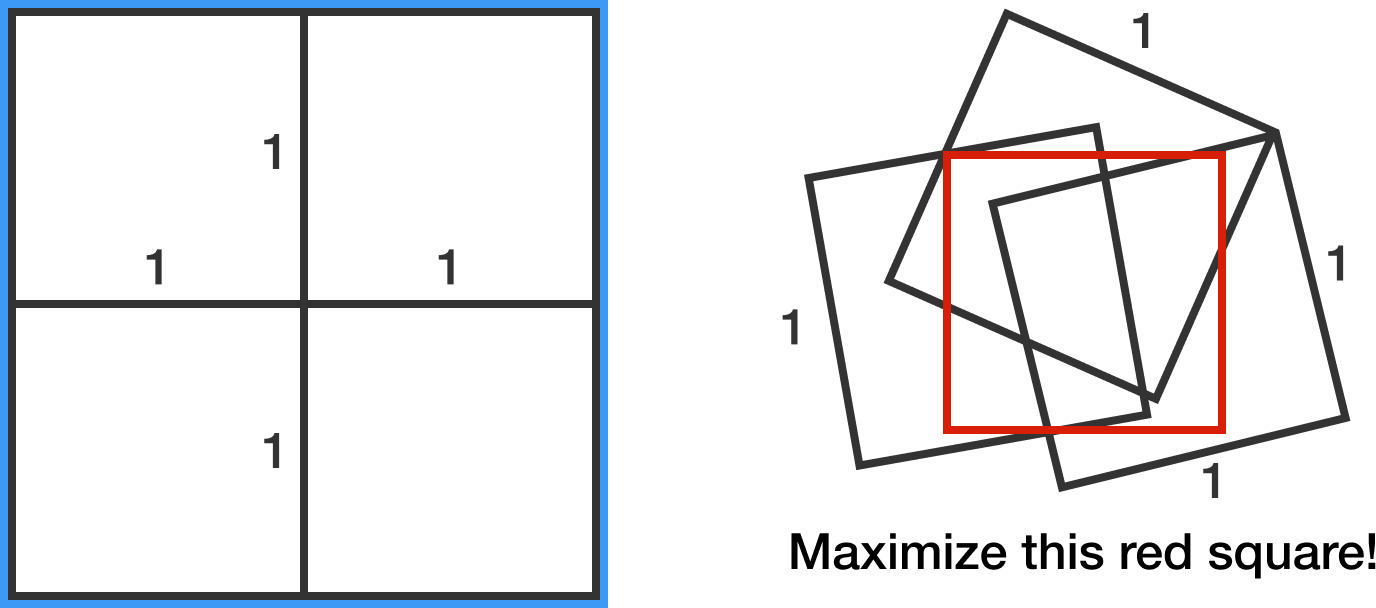
The largest square which can be covered completely with four unit squares is a square, as shown on the left.
Without cutting or bending the unit squares, what is the side length (to 3 decimal places) of the largest square that can be covered completely with three unit squares?
Disclaimer: The image on the right is not necessarily the right configuration to obtain the largest square.
The answer is 1.272.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
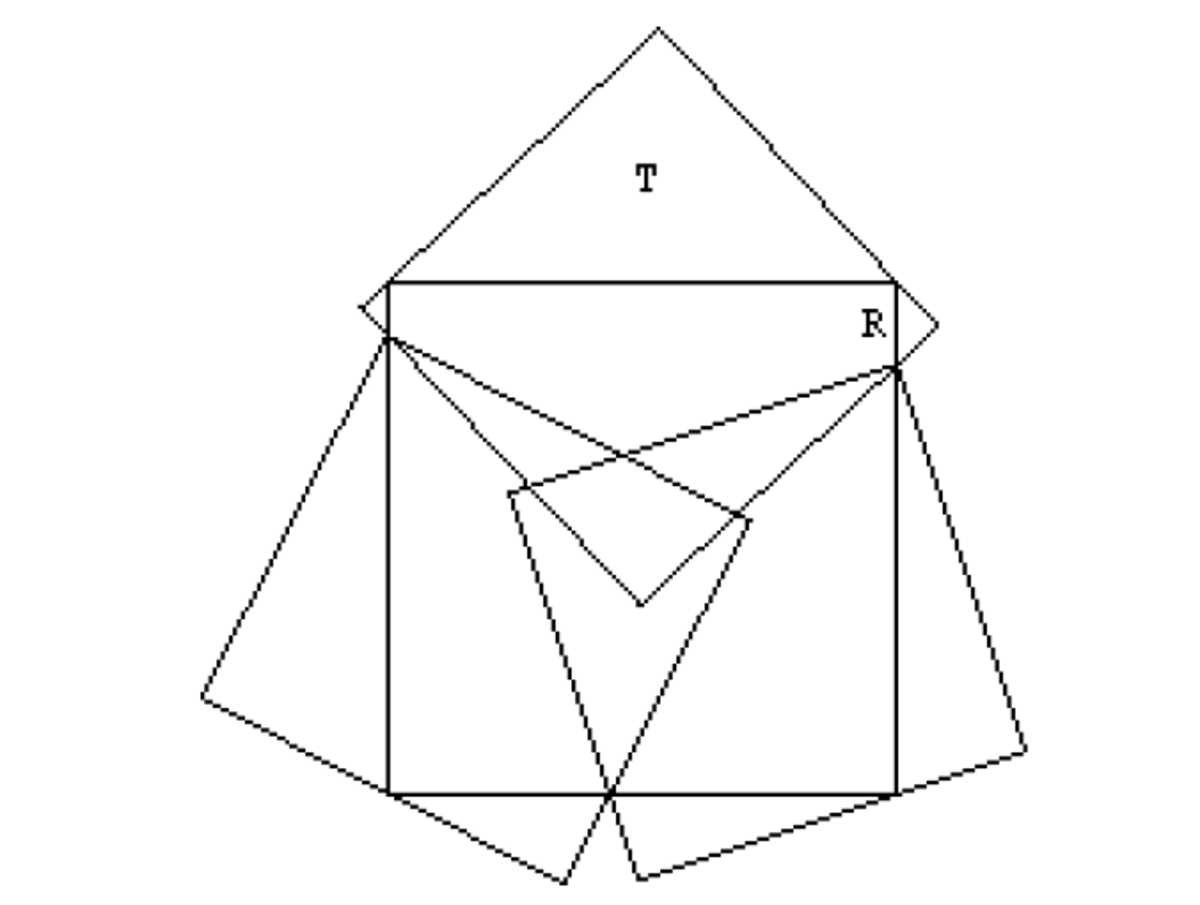
Any complete covering of a larger square by 3 unit squares is going to partition the perimeter of the larger square into at least 3 segments. Suppose one of them covers one segment. The maximum segment any one square can cover has a length of 2 , which occurs when one of the unit squares shares one same vertex with the larger square and is aligned with it---as the graphic shows. Then it's a matter of how much more the other two unit squares can cover.
If S is the side length of the larger square, and point P has the coordinates ( x , y ) , then if we let s = x y , point Q has the coordinates
Q = ( s 2 + 1 S , s s 2 + 1 S )
then we have the following system of equations to solve for x , y , s , S
x 2 + x 2 = 1
s = x y
− s 1 ( S − x ) + y = S − 1
( S − s s + 1 S ) 2 + ( s s s + 1 S ) 2 = 1
which yields the result
S = 2 1 + 5 = 1 . 2 7 2 0 2 . . .