Square Center from Four Points
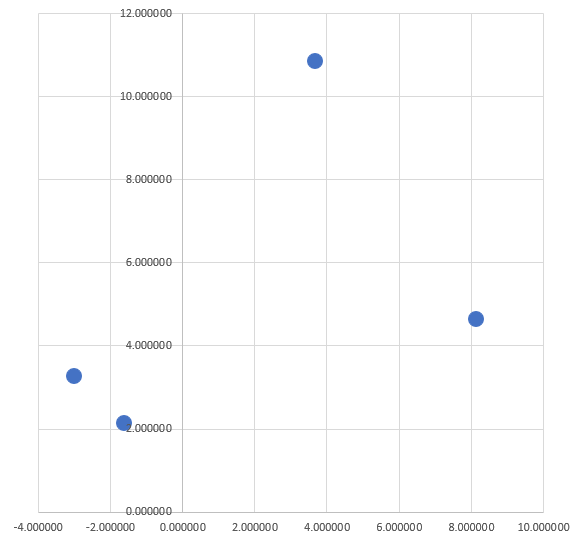
The following four points lie on a square in the x y plane (coordinates are approximate):
P 1 = ( x 1 , y 1 ) = ( 3 . 6 8 8 5 0 0 , 1 0 . 8 4 3 0 8 9 ) P 2 = ( x 2 , y 2 ) = ( − 3 . 0 0 3 3 5 2 , 3 . 2 7 5 4 5 3 ) P 3 = ( x 3 , y 3 ) = ( − 1 . 6 1 1 0 8 6 , 2 . 1 3 0 2 0 3 ) P 4 = ( x 4 , y 4 ) = ( 8 . 1 3 7 8 7 7 , 4 . 6 4 7 6 8 4 )
Determine the y -coordinate of the square's center.
Some additional information:
1)
The
x
-coordinate of the square's center is
3
.
2
2)
The square's side length is
1
0
3)
The square's sides are not necessarily parallel to the
x
and
y
axes
4)
The four points are not necessarily at the midpoints of the square's sides
5)
Each of the four points lies on a different side of the square
The answer is 5.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I have added an additional assumption about the points each being on different sides. Thanks for pointing that out
Log in to reply
I first tried having P 2 and P 3 on the same side. Then P 1 is on the opposite side of a square of side very nearly equal to 1 0 (about 1 0 . 0 5 6 , I recall), but the point P 4 is nowhere near that square.
Let us assume that the four points each lie on a different side of the square. The edges of the square will then be parallel to the unit vectors u = ( sin θ cos θ ) v = ( cos θ − sin θ ) for some θ . We then determine the value of θ by requiring that ( P 1 − P 3 ) ⋅ u = ( P 2 − P 4 ) ⋅ v = 1 0