Square circle square
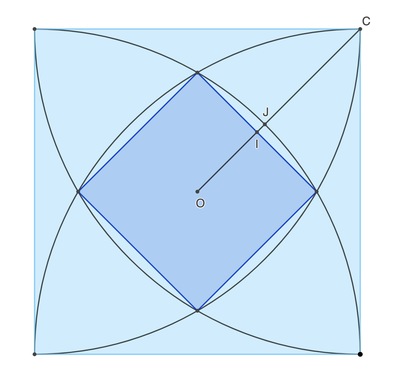
Four quarter circles are centered and terminate on the vertices of a square, as shown. A second, smaller square is defined by the intersections of the quarter circles. O is the center of the outer square. Find the ratio of the length of the segment I J to the side of the outer square. If this ratio is expressed as a a − a + a + 1 , submit a .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So I kinda cheated on this problem. Sorry :)
a a − a + a + 1 is always increasing from 0 to positive infinity, so we know that if we come across an answer that is obviously too big, all numbers above it will also be too big. We also know that a must be an integer (because the answer slot only accepts integers)
If a = 1 , then a a − a + a + 1 is negative, and if a = 3 , then a a − a + a + 1 is 0 . 2 5 . It is obvious that the ratio cannot be negative, and that I J is obviously not 4 1 of the outer square side length. Therefore, a must equal 2 .
And if we check, a = 2 gives a a − a + a + 1 ≈ . 0 3 , which makes logical sense.
Not cheating at all in my book. A man after my own heart in fact. :)
Let the side length of the outer square be 1 . Then the ratio 1 I J = I J = 1 − cos 1 5 ∘ . Since 2 cos 2 1 5 ∘ − 1 = cos 3 0 ∘ = 2 3 , ⟹ cos 1 5 ∘ = 2 2 + 3 and I J = 2 2 − 2 + 3 . Therefore a = 2 .