Square Composed of Triangles
A square composed of five triangles is given with unknown side lengths. Four triangle perimeters are given. What is the perimeter of the 5th triangle, P5=? Give your answer to the nearest 1/100th.
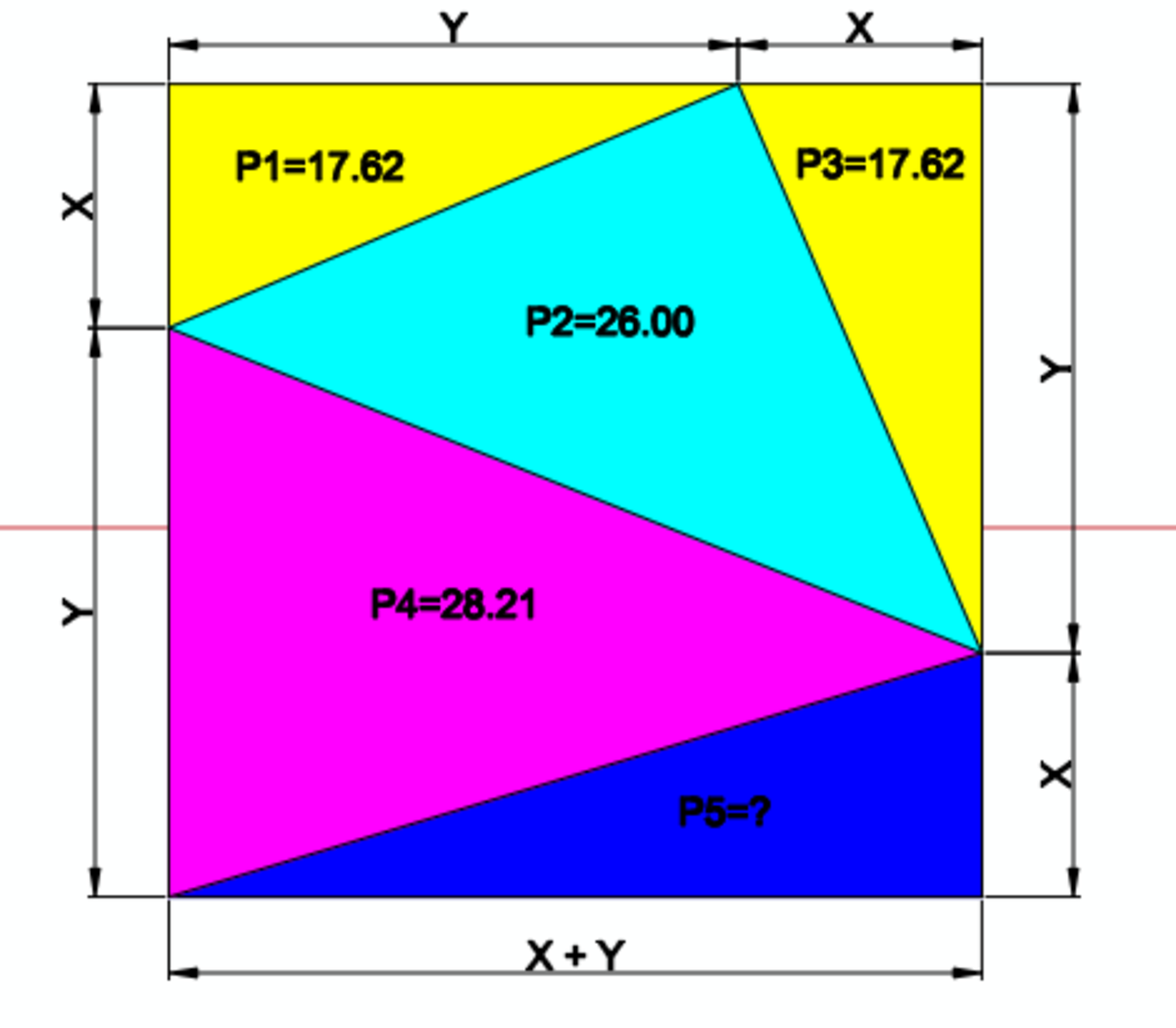
The answer is 23.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
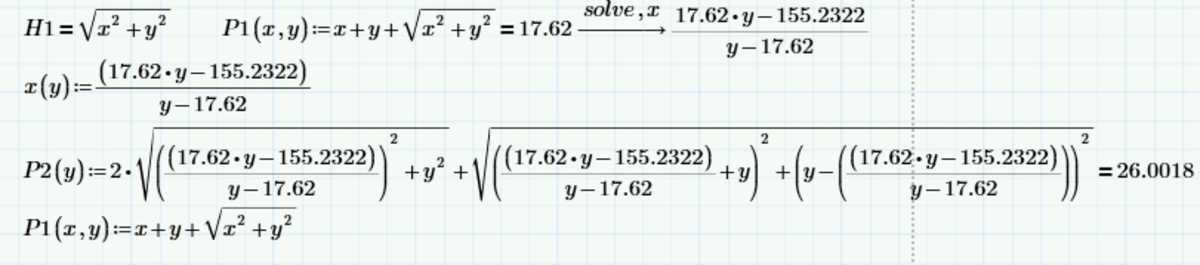

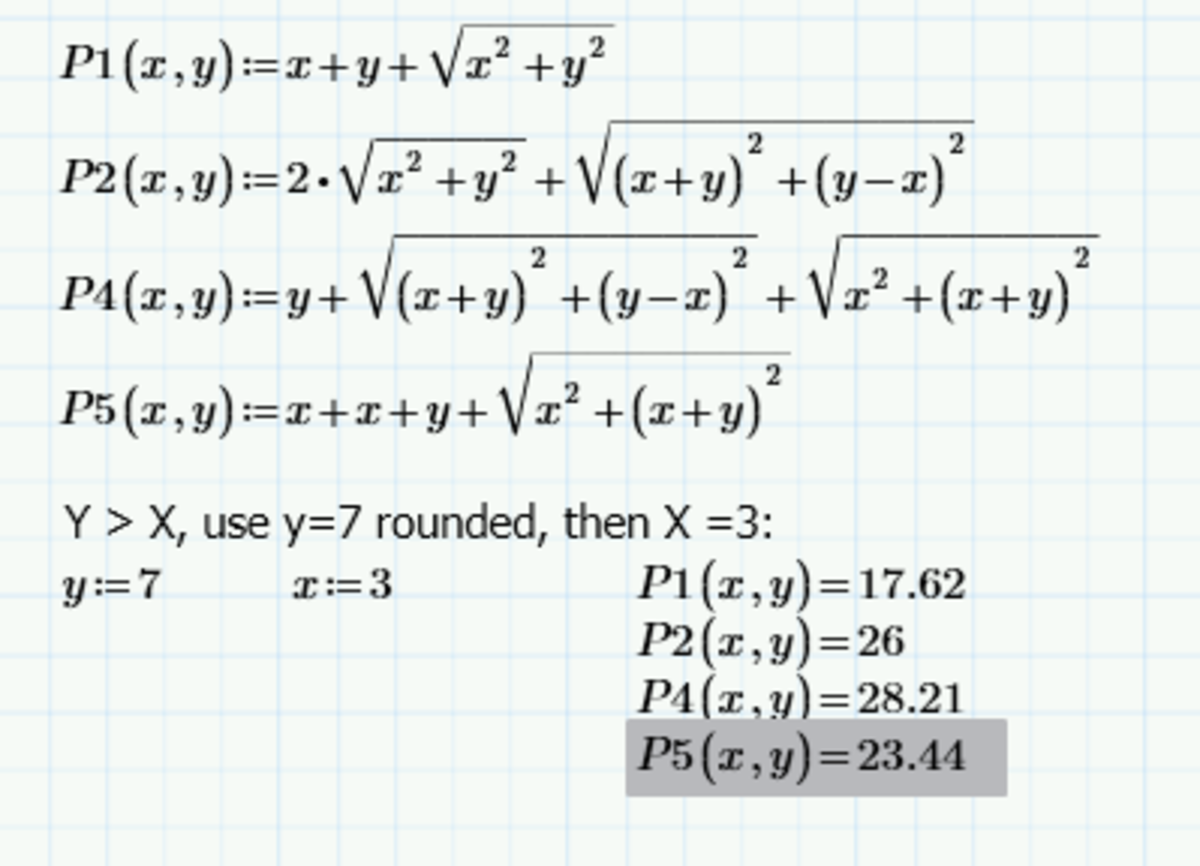
P1 & P3 are congruent triangles, while P2 is an isosceles right triangle. Therefore, P1's hypothenuse
= P3's hypothenuse
= 26 / (1 + 1 + √2)
= 26 / (2 + √2)
= 7.62
By this, X + Y
= { P1 (or P3), the perimeter } - 7.62
= 10.
P2's hypothenuse
= [ 26 / (1 + 1 + √2) ] × √2
= 26√2 / (2 + √2)
= 26 / (1 + √2)
= 10.77 = √[ (Y + X)² + (Y - X)² ]
(Y - X)² = 10.77² - 10²
= 0.77 × 20.77
= 15.99
≈ 16
Y - X = √15.99 ≈ 4
Y + X = 10
2Y = 14 ==> Y = 7 & X = 3
Answer, P5
= X + (Y + X) + √[ X² + (Y + X)² ]
= 3 + 10 + √[ 3² + (10)² ]
= 13 + √109
= 23.4403065
P/s : Those without a calculator can get √109 by using P4 and P2's hypothenuse, with 28.21 - Y - 10.77 = 28.21 - 7 - 10.77 = 28.21 - 17.77 = 10.44