Square Division
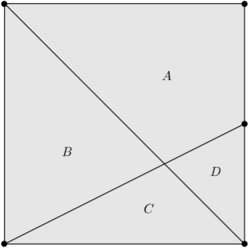 A diagonal is constructed in a square.
A diagonal is constructed in a square.
On the other pair of corners, a line is drawn from one of the two such that it intersects the midpoint of one of the opposite sides.
These two lines divide the square into four regions, A , B , C , D , in order from largest area to smallest area.
The ratio of these four areas can be expressed as a : b : c : d where a , b , c , d , are all integers and are setwise coprime, but not necessarily pairwise coprime.
Find a + b + c + d
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A very short and elegant solution! An alternative approach to the largest area would be to extend the midpoint bisector and the top side until they intersect, and analysing the resulting triangle formed
Log in to reply
Would you like to post it or would I post it as an alternative solution?
Log in to reply
It is a bit late here right now so you can post it if you want
C has twice the area of D, so (A+E):D = 8:1
E has the same area as C+D, and C is twice D, so E:D=3:1
Subtracting the ratios, we get A:D=5:1
You can continue from there.
WLOG, Let the square have side length one and the lower left corner be the origin. Then the diagonal has equation y = 1 − x and the second line has equation y = 2 x . These intersect where 1 − x = 2 x ⟹ x = 3 2 so they intersect at the point ( 3 2 , 3 1 )
Now:
b = 3 2 ⋅ 2 1 = 3 1
c = 3 1 ⋅ 2 1 = 6 1
d = 3 1 ⋅ 2 1 ⋅ 2 1 = 1 2 1
and a is the remainder of the square with area 1 meaning it must be 1 2 5
Multiplying through by 1 2 we have a : b : c : d = 5 : 4 : 2 : 1 meaning the answer is 5 + 4 + 2 + 1 = 1 2
Nice solution, using coordinates.
Very good approach. Congratulations.
The two lines trisect one another. Triangles C and D has the same height. So C=2D. Same with C and B. B=2C=4AD. A+D=B+C. So A=4D+2D-D=5D. A+B+C+D=5D+4D+2D+D= 1 2 ∗ D .
Are you really 87yrs old?
Log in to reply
1928 is the year.
Note that B and D are similar with ratio 2:1 [EH:MF=2:1], so their area is 4:1 [squared].
Since the edges of B and D are in ratio of 2:1, the diagonal [HJ:FJ] is divided into 2:1.
Therefore, B:C = 2:1.
From B:D=4:1 and B:C=2:1 we obtain C:D=2:1.
Since B+C is half the square, B+C= 2 1 , so B= 3 1 and C= 6 1 .
Since C:D=2:1, D= 1 2 1 .
Therefore, A = 1 − 3 1 − 6 1 − 1 2 1 = 1 2 5 .
Therefore, A:B:C:D = 1 2 5 : 3 1 : 6 1 : 1 2 1 = 5 : 4 : 2 : 1 .
Alternatively: (please enlarge this photo to view clearly)
Extend EM and HG to I.
Then, C is similar to (A+E) with a ratio 1:2, so the area ratio is 1:4 [squared].
And then?
Note: the [square brackets] are annotations.