Square geometry problem
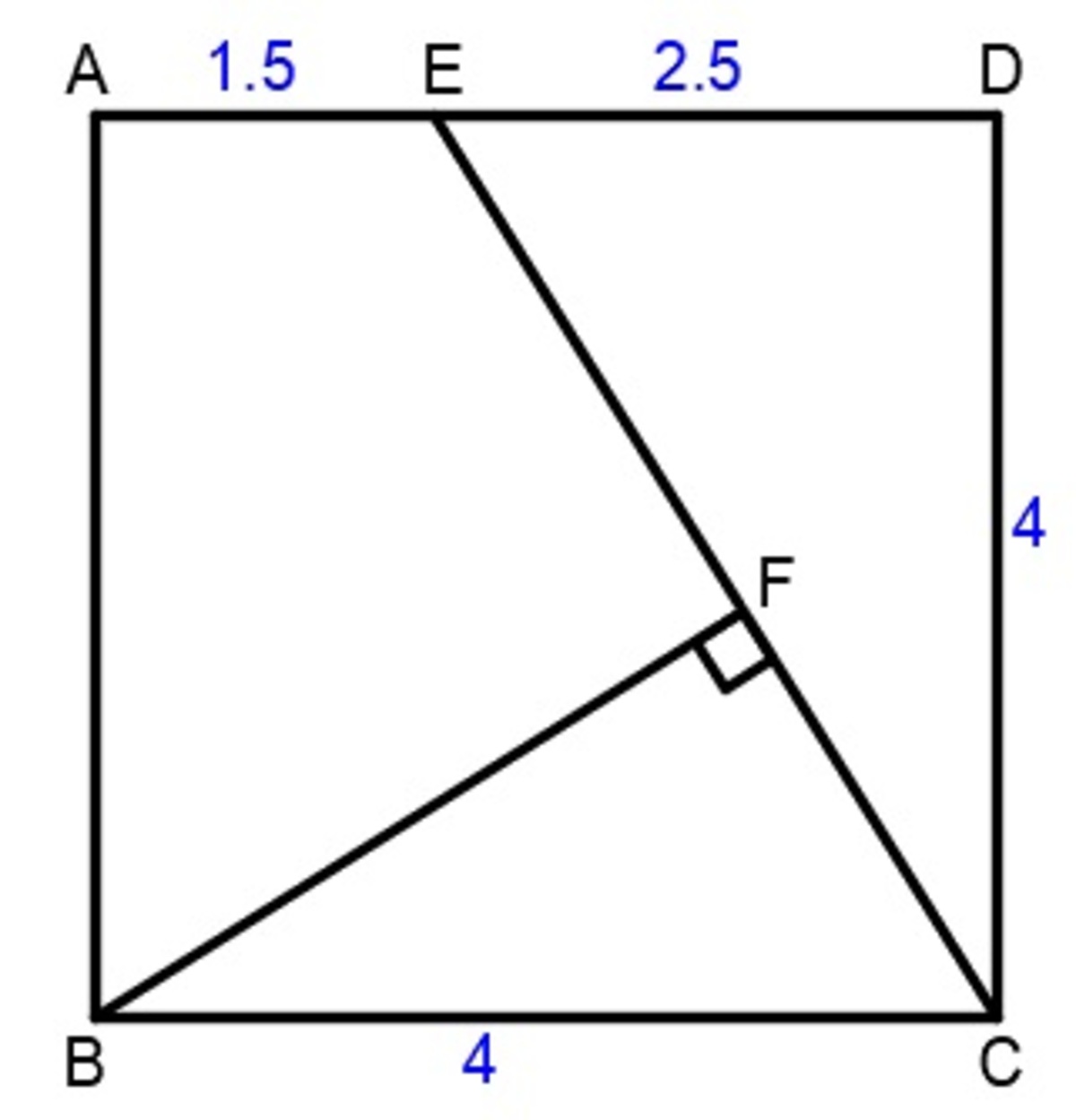
Square A B C D has a side of 4 c m . Point E lies on the side A D such that ∣ A E ∣ = 1 . 5 c m . What is the distance from the line E C to the point B ?
The answer is 3.39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Note:
Figure is not in scale
Using Pythagorean Theorem with △ C D E , we can see that E C = 4 2 + 2 . 5 2 = 2 2 . 2 5
Consider the area of △ B E C A r e a = 2 1 ( 4 ) ( 4 ) = 8
But at the same time, we can find the area with A r e a = 2 1 ( E C ) ( d ) = 8
Therefore, the perpendicular distance from B to line E C is d = E C 1 6 = 2 2 . 2 5 1 6 ≈ 3 . 3 9
Much more elegant than mine. Higher maths really gives you a blind eye to these kinds of solutions. :)
I solved it the same way as you.
 By pythagorean theorem, we have
By pythagorean theorem, we have
E C = ( E D ) 2 + ( C D ) 2 = 2 . 5 2 + 4 2 = 2 2 . 2 5
Since ∠ D E C = ∠ B C E , we have
B C B F = E C C D
4 B F = 2 2 . 2 5 4
B F = 2 2 . 2 5 4 ( 4 ) ≈ 3 . 3 9 2
My solution via analytic geometry:
At first, let's put our square into cartesian coordinate system, so that point A lies at the origin.
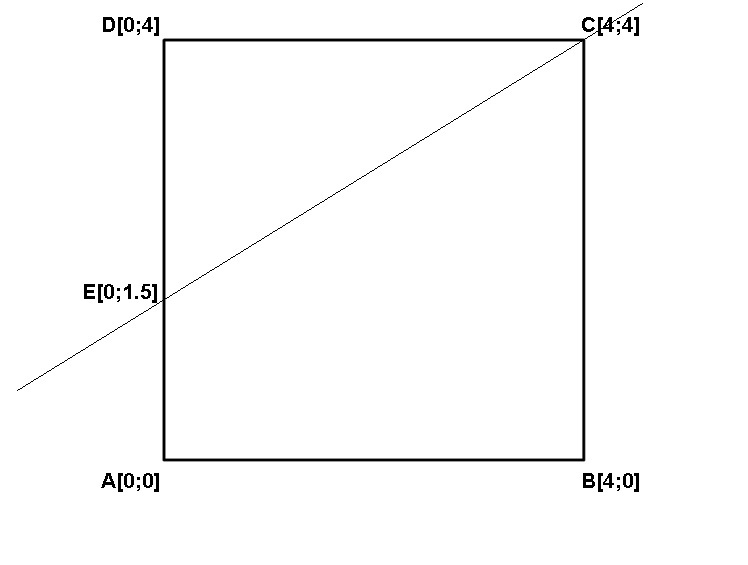 Line EC is defined:
p
:
E
[
0
;
1
.
5
]
,
C
[
4
;
4
]
and has a corresponding vector:
p
:
E
C
∈
p
,
E
C
=
(
4
−
0
;
4
−
1
.
5
)
=
(
4
;
2
.
5
)
General formula of a line is defined:
p
:
a
x
+
b
y
+
c
=
0
Where a and b are perpendicular to the directional vector:
p
:
n
⊥
E
C
=
(
2
.
5
;
−
4
)
By plugging one of points lying on the line, we get
c
:
p
:
E
∈
p
,
E
[
0
;
1
.
5
]
p
:
2
.
5
x
+
(
−
4
)
y
+
c
=
0
p
:
2
.
5
×
0
+
(
−
4
)
×
1
.
5
+
c
=
0
p
:
c
=
6
So the full general formula of a line looks like this:
p
:
2
.
5
x
+
(
−
4
)
y
+
6
=
0
While having a general formula of a line and coordinates to the point, for which we want to know the distance to, we can use a distance formula:
v
(
B
,
p
)
=
a
2
+
b
2
∣
a
×
b
1
+
b
×
b
2
+
c
∣
Where:
B
[
b
1
;
b
2
]
,
p
:
a
x
+
b
y
+
c
=
0
So the solution is:
v
(
B
,
p
)
=
2
.
5
2
+
(
−
4
)
2
∣
2
.
5
×
4
+
(
−
4
)
×
0
+
6
∣
∼
4
.
7
1
6
.
.
.
1
6
∼
3
.
3
9
c
m
And we can also check our solution graphically:
Line EC is defined:
p
:
E
[
0
;
1
.
5
]
,
C
[
4
;
4
]
and has a corresponding vector:
p
:
E
C
∈
p
,
E
C
=
(
4
−
0
;
4
−
1
.
5
)
=
(
4
;
2
.
5
)
General formula of a line is defined:
p
:
a
x
+
b
y
+
c
=
0
Where a and b are perpendicular to the directional vector:
p
:
n
⊥
E
C
=
(
2
.
5
;
−
4
)
By plugging one of points lying on the line, we get
c
:
p
:
E
∈
p
,
E
[
0
;
1
.
5
]
p
:
2
.
5
x
+
(
−
4
)
y
+
c
=
0
p
:
2
.
5
×
0
+
(
−
4
)
×
1
.
5
+
c
=
0
p
:
c
=
6
So the full general formula of a line looks like this:
p
:
2
.
5
x
+
(
−
4
)
y
+
6
=
0
While having a general formula of a line and coordinates to the point, for which we want to know the distance to, we can use a distance formula:
v
(
B
,
p
)
=
a
2
+
b
2
∣
a
×
b
1
+
b
×
b
2
+
c
∣
Where:
B
[
b
1
;
b
2
]
,
p
:
a
x
+
b
y
+
c
=
0
So the solution is:
v
(
B
,
p
)
=
2
.
5
2
+
(
−
4
)
2
∣
2
.
5
×
4
+
(
−
4
)
×
0
+
6
∣
∼
4
.
7
1
6
.
.
.
1
6
∼
3
.
3
9
c
m
And we can also check our solution graphically:
We place the square in the coordinate plane as shown below:
The slope of segment EC is 2 . 5 4 = 5 8 ; thus EC lies along the line y − 4 = 5 8 ( x − 4 ) , which can be re-written as 8 x − 5 y − 1 2 = 0 .
The distance D from a point ( x 0 , y 0 ) to the line A x + B y + C = 0 is given by
D = A 2 + B 2 ∣ ∣ ∣ A x 0 + B y 0 + C ∣ ∣ ∣
Thus in our case the distance from B ( 0 , 4 ) to 8 x − 5 y − 1 2 = 0 is
d = 8 2 + ( - 5 ) 2 ∣ ∣ ∣ 8 ( 0 ) − 5 ( 4 ) − 1 2 ∣ ∣ ∣ = 8 9 3 2 ≈ 3 . 3 9