Square house with square patches

Geometry Level 1

My house (in white) and four square gardens (in green) are built on a square land of $400\text{ m}^2.$

What is the perimeter of my house?

60 \text{ m}

80 \text{ m}

100 \text{ m}

120 \text{ m}

7 solutions

Jordan Cahn
Oct 8, 2018

Note that in each square garden, the combined length of the two solid lines equals the combined length of the two dashed lines. Thus, the perimeter of the house with the gardens is the same as the perimeter of the square plot of land.

Since $\sqrt{400}=20$ , each side of the square has length 20 and the perimeter is $\boxed{80\text{ m}}$

Perimeter is 80m not 80m^2

A Former Brilliant Member - 2 years, 7 months ago

The question was changed (slightly) from when I first answered it (the initial question had an area for its answer). My answer has been updated.

Jordan Cahn - 2 years, 7 months ago

Perimeter is measured with length so it will be 80m. Kindly change 80m^2 to 80m.

Venkatachalam J - 2 years, 7 months ago

That's what I think about.(There is just one way to solve this problem right?)But I like your thinking too

Qiao Qiao - 2 years, 7 months ago

2(Length+width)=perimeter

Abdullah Sakhi - 1 year, 5 months ago

Venkatachalam J
Oct 28, 2018

Relevant wiki: Length and Area Problem Solving

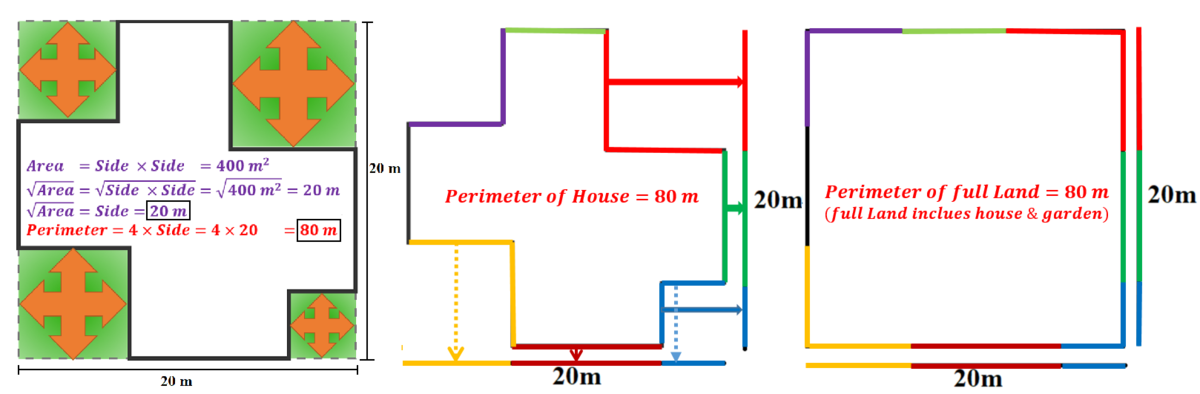Area of square land equal to 400 square meters. Hence, the side length of the square land equal to 20m and the perimeter of the square land equal to 80m. Each of the square gardens dashed lines and parallel bold lines are equal. Therefore, the perimeter of the house equal to perimeter of the square land .

Note: The solution remain same, if the corners of square land has square (or) rectangular (or) mix of square and rectangular garden. Since, square and rectangle has four right angles and length of opposite sides of dashed lines and corresponding bold lines are equal.

As can be seen from your solution, the gardens could also be rectangular without affecting the answer.

As a small point for improvement: why are the dashed and bold lines that are parallel the same length? In this case it's thanks to the right angles. If they wouldn't be squares but 80-90-90-100 quadrilaterals this trick wouldn't work. But for parallelograms it would also work. So it is because both pairs of opposing sides of the garden areas are parallel that the opposite sides are of identical length.

Roland van Vliembergen - 2 years, 7 months ago

Priti Gupta
Oct 8, 2018

Good question. I was bamboozled at the first instance...

Ok I solved it as follows:

GIVEN Area: 400

Therefore, side=20

Therefore perimeter of land = 80

Intuition followed next

(last piece of info was the presence of square garden so try to replace sides and switch stuff)

Hence the answer

I was "bamboozled," too, for several seconds.

Linda Slovik - 2 years, 7 months ago

I was bamboozled for a WHILE. :-) Sadly, being bamboozled over math problems has plagued me for most of my life. I very much envy math wizards.

Jesse Otis - 2 years, 7 months ago

Thanks for the solution

Lovin Jose - 2 years, 7 months ago

Sorin Stefan
Nov 3, 2018

I solved it intuitively as a limit problem. If the four green squares are infinitely small, the house will equate the big square iself, 80 m. Whatever size the small squares have, the result is always the same.

Bernard Zimmermann
Oct 31, 2018

You presented earlier a problem similar to this one and I remembered the answer

Ervyn Manuyag
Oct 28, 2018

Square root of 400=20 and 20x4=80

Vivek Sharma
Oct 28, 2018

Each side of the large square is 20m, area being 400m^2 , the garden squares have similarly two adjacent sides are equal to dashed margins. Thereby the perimeter of the house remaining the same as it would have been if it was a perfect square. Hence the perimeter is 4x 20 = 80m

Square house with square patches

7 solutions

0 pending reports