Square in a Circular Sector
A circular sector with central angle 1 2 0 ∘ is shown in the diagram. We want to place a square in it symmetrically, as indicated in red.
If the radius of the circular sector is 1 0 0 , what is the side length of the square?
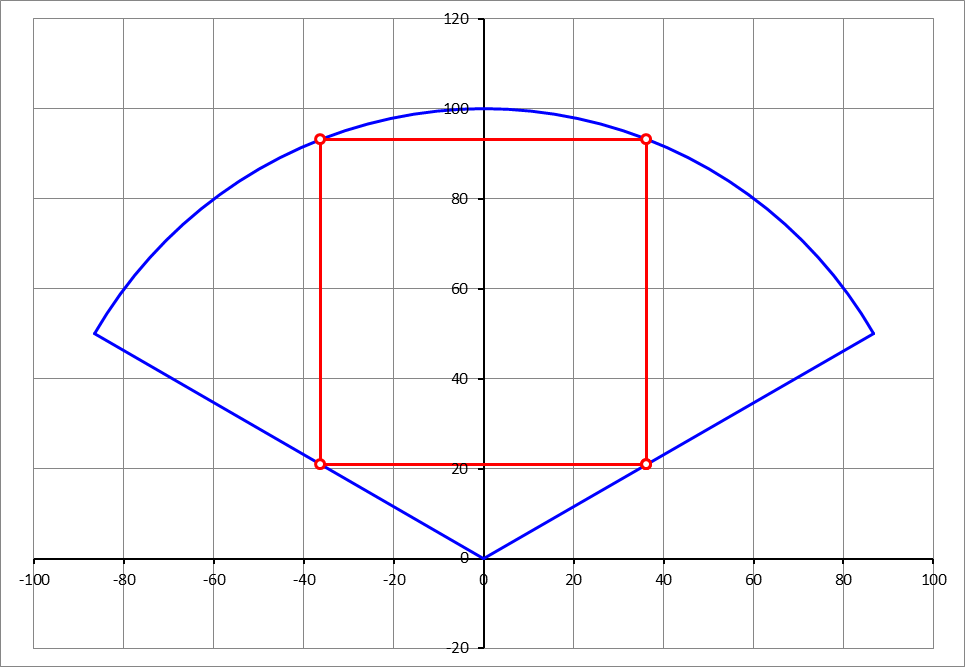
The answer is 72.34451538.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
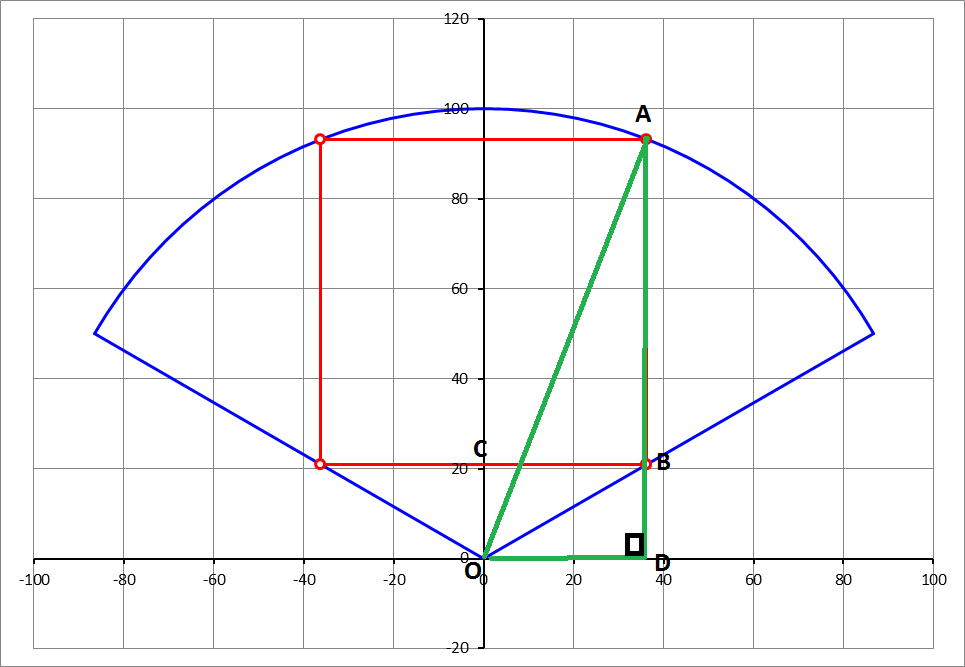
Let the side length of the square be 2a. Let A and B be the points where the top-right and the bottom-right corner of the square intersect the sector, O be the origin, C be the point where the Y-axis intersects the square initially. Extend AB to meet the X-axis at D.
∠ C B O = 9 0 - 2 1 2 0 = 3 0
Since the square is placed symmetrically, C B = 2 2 a = a .
O C = B D = a × t a n 3 0 = 3 a .
A D = A B + B D = 2 a + 3 a .
O D = C B = a .
A O =radius of the sector= 1 0 0 .
By the Pythagorean Theorem,
A D 2 + O D 2 = A O 2
( 2 a + 3 a ) 2 + a 2 = 1 0 0 0 0
Solving we get, 2 a ≈ 7 2 . 3 4 4 5
Assume the sector to be a part of the circle: x²+y²=100². Let (p.q) be a point on the right hand side straight line, y= √ 3 x . Or q(√3)=p. Further let x be the side of the square; then x=2p & (p,q+x) lies on our circle. Hence, p²+(q+x)²=100². On substitution one obtains, x= √ ( 4 + √ 3 ) 1 0 0 √ 3 = 72.3445