Square in a Quarter Ellipse
Take the ellipse
in the first quadrant, and inscribe a square in it, such that one corner of the square is the -axis, one on -axis, and two corners are on the ellipse, as shown in the figure below.
If the side length of the square is , its center is at , and its clockwise tilt is (in degrees), then input the value of . You may need to resort to numerical methods.
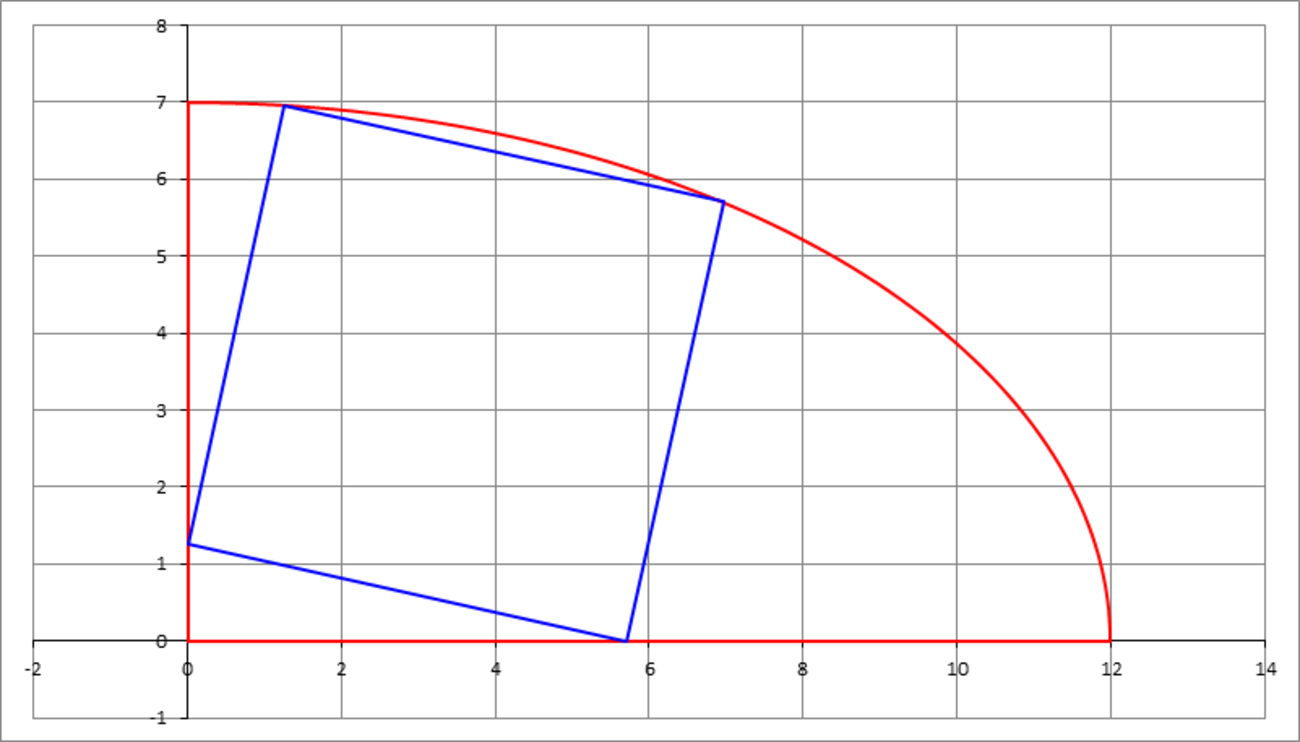
The answer is 25.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider the general case, where the ellipse has semimajor and semiminor axes a , b . Say the two points on the curve are P ( a cos u , B sin u ) , Q ( a cos v , b sin v )
where u > v (so P is the point closer to the y -axis), and define R and S as below:
Since P Q R S is a square, the difference in the y -coordinates of points Q and R is the same as the difference in the x -coordinates of Q and P , etc; so we have R ( a cos v − b sin u + b sin v , b sin v − a cos v + a cos u ) and S ( a cos u − b sin u + b sin v , b sin u − a cos v + a cos u )
Since R is on the x -axis and S on the y -axis, we have b sin v − a cos v + a cos u a cos u − b sin u + b sin v = 0 = 0 from which we see that a cos v = b sin u so we can write v in terms of u ; in particular sin v = 1 − a 2 b 2 sin 2 u
Substituting into the second equation above, we get a cos u − b sin u + b 1 − a 2 b 2 sin 2 u = 0
We could solve this numerically for u here; but amazingly, it is solvable analytically. If we let x = sin u (so that cos u = 1 − x 2 ) and clear square roots, we find that x is a root of ( a 4 − a 2 b 2 + b 4 ) ( a 4 + 3 a 2 b 2 + b 4 ) x 4 − 2 a 2 ( a 6 + b 6 ) x 2 + a 4 ( a 2 − b 2 ) 2 = 0
This looks bad, but is just a biquadratic in x (that is, a quadratic in x 2 ). In this case, the a = 1 2 and b = 7 and the polynomial is 7 1 2 4 6 8 7 0 5 x 4 − 8 9 3 8 4 6 3 0 4 x 2 + 1 8 7 1 4 2 4 0 0 = 0
The root we want is x = 1 2 4 4 3 0 5 1 9 3 + 4 4 3 0 5 1 6 0 8 1 1 4 1 1 2
From this we can calculate u , v , the coordinates of the vertices of the square, and all the parameters we need for the solution; we find s = 5 . 8 3 2 2 9 , C x = C y = 3 . 4 8 0 6 6 , θ = 1 2 . 4 5 7 0 8 ∘ for a total of 2 5 . 2 5 7 6 4 … .