Square in a semicircle

Geometry Level 2

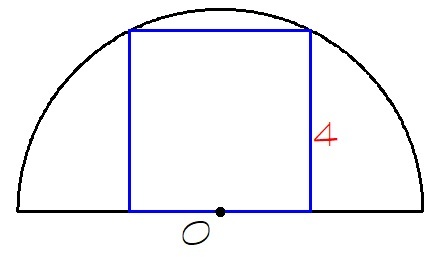
A square of perimeter $16$ is inscribed in a semicircle, as shown.

Find the perimeter of the semicircle rounded to the nearest integer.

Use $\frac{22}{7}$ for the approximation of $\pi$ .

14 15 23 31

1 solution

A Former Brilliant Member
Oct 27, 2017

Let $r$ be the radius of the semicircle. Using the pythagorean theorem , we have

$r^2=4^2+2^2$ $\implies$ $r=\sqrt{20}=2\sqrt{5}$

The perimeter of the semicircle is half the circumference plus twice the radius. We have

$p=\dfrac{1}{2}(2\pi r)+2r=\dfrac{22}{7}(2\sqrt{5})+2(2\sqrt{5})=$ $\boxed{23}$

I could not understand why are we adding 2r as well

Devjit Ghosh - 11 months, 2 weeks ago

You have to account for the bottom of the semicircle, which is a line with length 2r.

Chace Caven - 8 months, 3 weeks ago