This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
x = 2 + 3 + 2 − 3 x 2 = ( 2 + 3 ) 2 + 2 ( 2 + 3 ) ( 2 − 3 ) + ( 2 − 3 ) 2 x 2 = 2 + 3 + 2 ( 4 − 3 ) + 2 − 3 x 2 = 2 + 2 + 2 = 6
hey dude, you might wanted to ask x 2 but you have put up the picture asking the value of x... so better change it!
now coming to the question, in this we have got to find x 2 rather than x..
 da
da
okay thx for the feedback
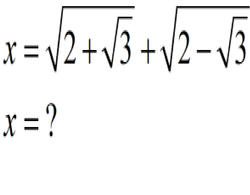
2 + 3 = 2 3 + 2 ⋅ 3 + 1 = 2 ( 3 + 1 ) 2 = 2 3 + 1
Similarly, we have
2 − 3 = 2 3 − 1
Hence,
x = 2 3 + 1 + 2 3 − 1 x = 2 2 ⋅ 3 a = x 2 = 6