Square in Right-angled Triangle
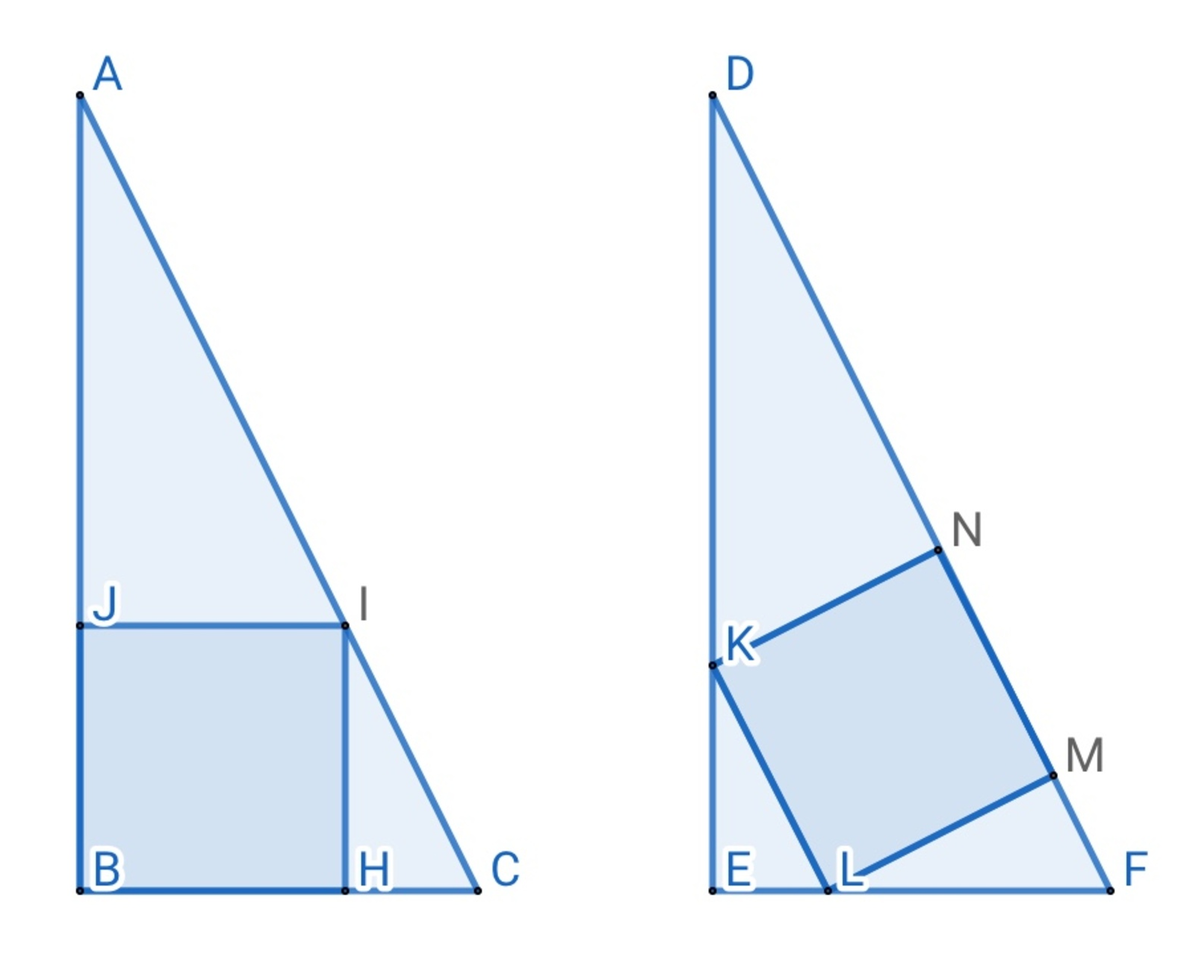
△ A B C and △ D E F below are congruent triangles, with ∠ A B C = ∠ D E F = 9 0 ° . Now we know A B = 4 , B C = 3 , both B H I J and K L M N are squares, H , I , J are points on B C , A C , A B and K , L , M , N are points on D E , E F , D F , D F .
Question: Which of the following two squares is smaller ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Edward Christian , I have amended you problem statement. We do not need to use unit of length in Geometry problems. You also did not use it in your solution. I have added another answer option □ B H I J = □ K L M N . The squares actually look equal in your figure.
Log in to reply
Ok, sir. I shall edit the explanation. Thanks for your advice.
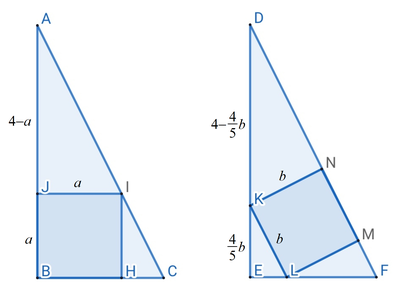
We note that all the seven triangles involved are 3 - 4 - 5 right triangles.
Let the side length of square B H I J be a . Since △ A J I is a 3 - 4 - 5 right triangle, J I A J = a 4 − a = 3 4 ⟹ 1 2 − 3 a = 4 a ⟹ a = 7 1 2 .
Similarly, let the side length of square K L M N be b , Then K E = 5 4 b and D K = 4 − 5 4 b and K N D K = b 4 − 5 4 b = 3 5 ⟹ 1 2 − 5 1 2 b = 5 b ⟹ b = 3 7 6 0 < 3 5 6 0 = 7 1 2 = a .
Therefore, [ B H I J ] < [ K L M N ] .
In square B H I J , ∠ B J I = 9 0 ° ∴ ∠ A J I = 1 8 0 ° − ∠ B J I = 1 8 0 ° − 9 0 ° = 9 0 ° ∵ ∠ A B C = 9 0 ° ∴ ∠ A B C = ∠ A J I
∵ ∠ B A C = ∠ B A C ∴ △ A J I ∼ △ A B C ∴ A B A J = B C I J ∴ 4 4 − x = 3 x ∴ x = 7 1 2
Made O E ⊥ D F , and the junction of O E and D F is O , of O E and K L is P .
In right-angled triangle R t △ D E F , from Pythagorean theorem, easily gets D F = D E 2 + D F 2 = 3 2 + 4 2 = 5
In right-angled triangle R t △ D E F , from the area, S △ D E F = 2 D E ⋅ D F = 2 D F ⋅ O E ∴ 2 5 ⋅ O E = 2 3 × 4 ∴ O E = 5 1 2 .
In square K L M N , O P = K L = y , K L ∥ M N ∴ K L ∥ D F ∴ ∠ E D F = ∠ E K L .
∵ ∠ D E F = ∠ D E F ∴ △ E K L ∼ △ E D F ∴ O E E P = D F K L ∴ 5 1 2 5 1 2 − y = 5 y ∴ y = 3 7 6 0
∵ x = 7 × 5 1 2 × 5 = 3 5 6 0 > 3 7 6 0 ∴ x > y ∴ Area Square BHIJ > Area Square KLMN □