Square In Circle in Square
 In a large square, the incircle is drawn (with diameter equal to the side length of the large square).
In a large square, the incircle is drawn (with diameter equal to the side length of the large square).
In the circle, a smaller square is inscribed.
What is the ratio of the area of the smaller square to the area of the larger square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Actually, this is similar to the triangle in circle in triangle problem, where rotating the inner square would give a quick visual solution.
The diagonal of the inner square is the diameter of the circle, which in turn is the side length of the outer square. So if a is the inner square's side length and is the outer square's side length, then
Let the diameter of circle be d and a side of the smaller square be s .
Area of smaller circle = s 2
Diagonal of Smaller Square = Diameter of circle = d
By Pythagoras theorem, d 2 = s 2 + s 2 = 2 s 2
Side of Bigger Square = d
Thus, area of Bigger Square = d 2 = 2 s 2
Ratio of their Areas is = 2 s 2 s 2 = 2 1
Good job! Thanks for writing a solution.
Please edit the solution, its not the area of the "smaller circle" but "smaller square".
rotate the inner square by 45 deg so that it appears as a rhombus whose diagonal length is equal to the side length of the bigger square.
Let the side length be a then area of bigger square is a^2 and the area of smaller square can be given by 1/2 a^2
which gives the ratio 1/2
Yes, the rotation makes the solution immediate :)
If you rotate the Red Square 45 Degrees you can see it is half the size of Green Square


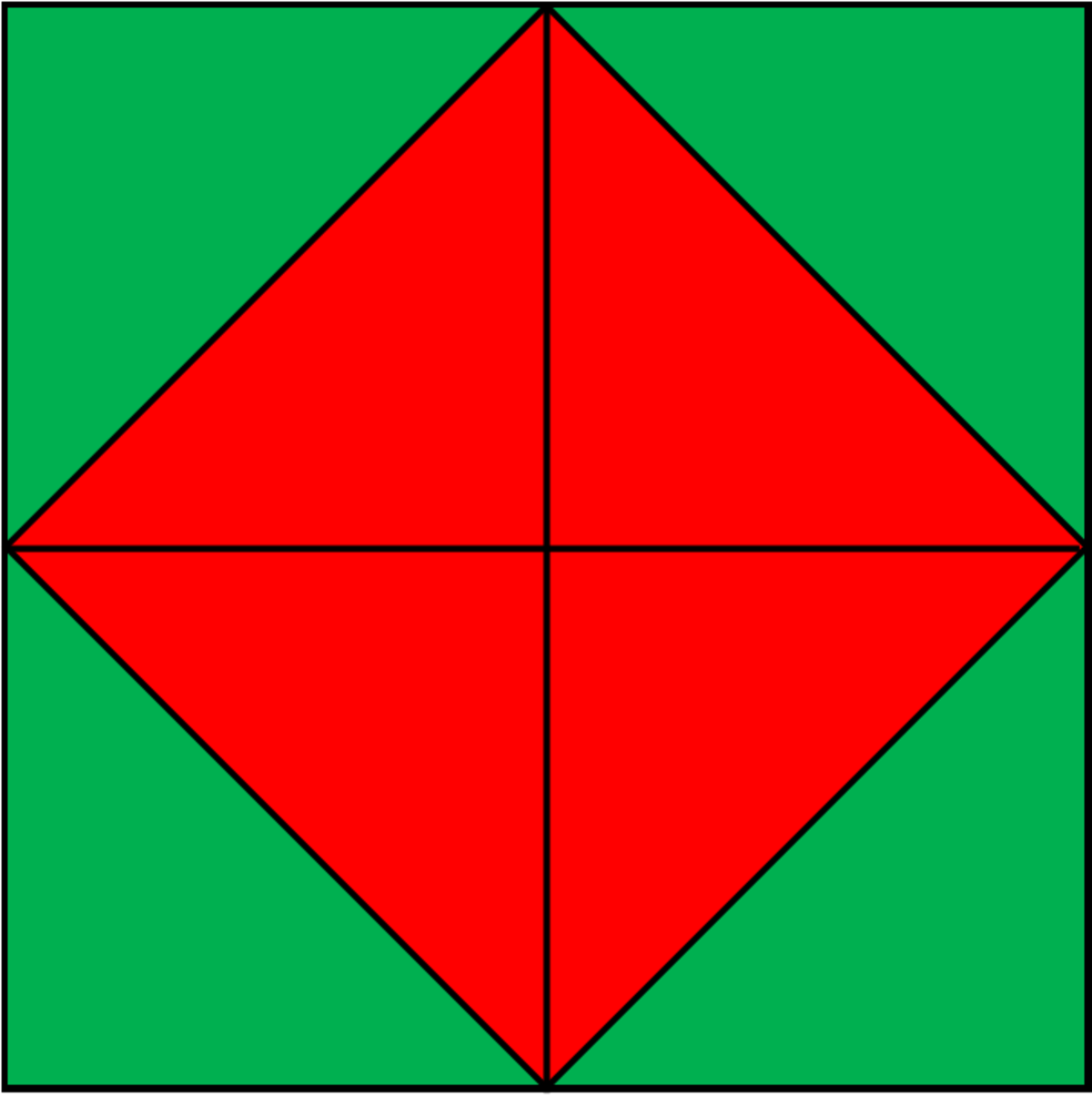
Yes, that's how I solved it! Thank you for your sharp images!
You can simply rotate the inner square 45 degrees (so it appears as a diamond with each vertex at the mid point of each side of the large square).
Looking at the newly constructed picture allows you to see that
Area of big square - area of 4 triangles = area of diamond (tilted square)
For notation, a = inner square side length and b = outer square side length
Area of 1 triangle = (1/8) b^2
Area of large square = b^2
Area of 4 triangles = (1/2)b^2
b^2 - (1/2)b^2 = (1/2)b^2
Since area of 4 triangles is equal to area of smaller square, and area of big square is the sum of the areas of 4 triangles + area of smaller square, 2 * smaller square = larger square
Therefore, the ratio of the area of the smaller square to larger square is 1:2
The rotation makes it a much easier problem :)
The diagonal of smaller cube is equal to the diameter of circle and the diameter of circle is equal to the side of larger cube. Now,it can be solved.
These are squares, not cubes. But otherwise, good solution.
Let the side length of the large square be x
Then , its area = x^2
The diagonal of the small square = x
Then its area = (x^2)/2
So
The ratio = 1 : 2
For convenience, let's take the side of the larger square to be of 6 units. Area of the square would be 3 6 s q . u n i t s .
Diameter of the circle will also be 6 units, therefore radius will be 3 units.
Since, we got the radius to be 3 units, the diagonal of the smaller square is 6 units.
Considering any one of the right triangles in the smaller square, we get s i n 4 π = 6 s i d e ⟹ s i d e = 3 2 u n i t s .
Therefore area of the smaller square is ( 3 2 ) 2 = 1 8 sq.units.
Now, taking the ratio of the areas of the squares, we get 3 6 1 8 = 2 1
Can be done in the same way by taking a general length a of the larger square.
Rotate the inner square by 45 degrees, then it is obvious by inspection.
Clearly the diameter of the incircle is equal to the side of big sq. And hypotenuse of the small sq. Therefore, [hyp of small sq. = side of big. Sq.]. Now, if hyp. Of smaller sq. Is √2a if sides are taken "a", hence the sides of bigger sq. Will be √2a therefore, ratio of areas will be =>{ a^2/(√2a)^2} i.e. 1:2.......... :)!
The green and yellow areas fit together to make a square the same size as the red square in the middle. This means the outside area of the green and yellow is equal to the red area. So 2 red squares equals the area of the original green square (ratio 1:2).
I just thought it looked like half so i chose that ratio and got it right....
Here's just another way to do it:
Plug in any numbers.
Big square: 8 * 8
Because the circle's diameter is 8, the small square's diagonal is 8.
You have to use the Pythagorean Theorem at this point.
The two sides are equal, so we know 2x^2=64.
x = (32)^1/2
Now, multiple x by itself to get the area of the small square. You end up with 32 :
64, which is really just 1 : 2 simplified.
Yay, math.
the diagonal of the the small square equals the side length of the large square equals the diameter of the circle = 2 x the area of the small square = 2 x^2 the area of the large square = 4 x^2 the ratio = 1/2
Thanks for writing a solution!
The diameter of the circle is equal to the side of the larger square and equal to the diagonal of the smaller square.
The diameter of circle=length side of larger square=the diagonal length of smaller square. So if r is the radius of circle, A is the side length of larger square and, 'a' is side length and 'd' is the diagonal of smaller square.then 2*r=A=d,
a^2+a^2=d^2,
2*a^2=d^2,
2*a^2=A^2 ,so
ratio of area of smaller square to larger square=a^2/A^2
=1/2
The diagonal of the inner square is the diameter of the circle, which in turn is the side length of the outer square. So if a is the inner square's side length and b is the outer square's side length, then b = a 2 + a 2 = a 2 ⇒ b 2 = 2 a 2 ⇒ b 2 a 2 = 2 1