Square inscribed in a triangle
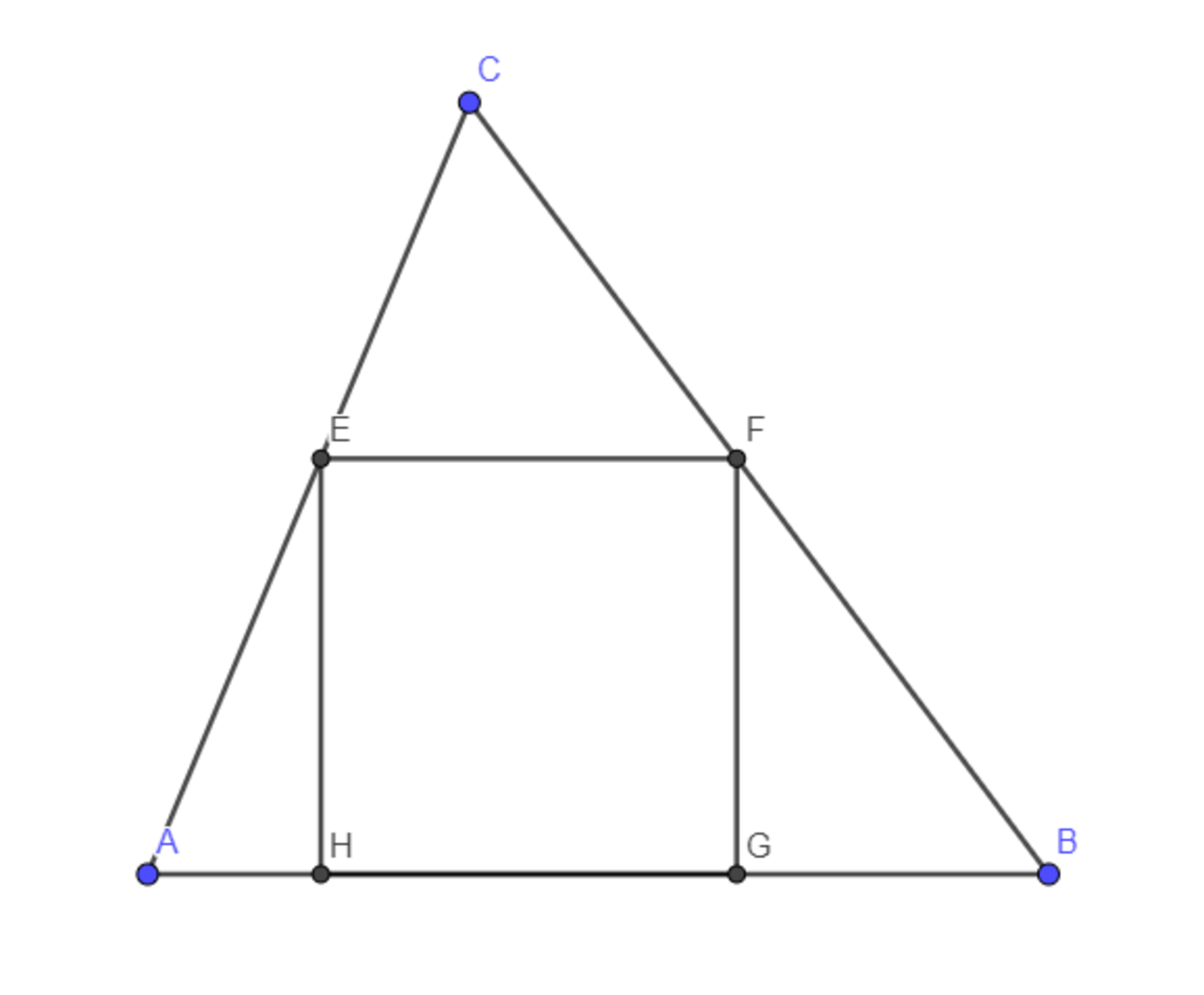
In △ A B C , A B = 1 4 , A C = 1 3 , B C = 1 5 . Square E F G H is inscribed in the triangle as shown in the figure above. The side length of the square is given by s = q p for some positive coprime integers p and q . Find p + q .
The answer is 97.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By Heron's Formula, the area of the triangle is A = 2 1 ( 2 1 − 1 3 ) ( 2 1 − 1 4 ) ( 2 1 − 1 5 ) = 8 4 , so its height is h = b 2 A = 1 4 2 ⋅ 8 4 = 1 2 .
By Cavalieri's principle the square will also be inscribed by a right triangle of the same height.
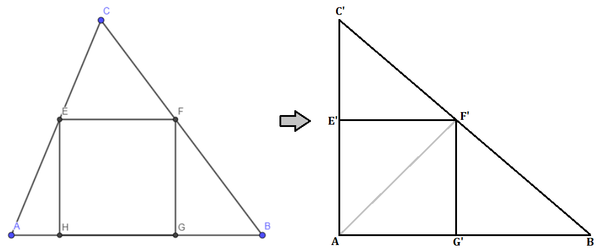
If the right angle is at the origin, then the hypotenuse of the right triangle will be on y = − 7 6 x + 1 2 , and the diagonal of the inscribed square will be on y = x .
These two equations intersect at x = 1 3 8 4 , the side length of the square. Therefore, p = 8 4 , q = 1 3 , and p + q = 9 7 .
A special feature of 13-14-15 triangle is that it is made of two Pythagorean triple triangles 5-12-13 and 9-12-15. It has a height C N of 12. Since △ C E F and △ A B C are similar, we have:
A B E F 1 4 s 6 s ⟹ s = C N C M = 1 2 1 2 − s = 8 4 − 7 s = 1 3 8 4
Therefore p + q = 8 4 + 1 3 = 9 7 .