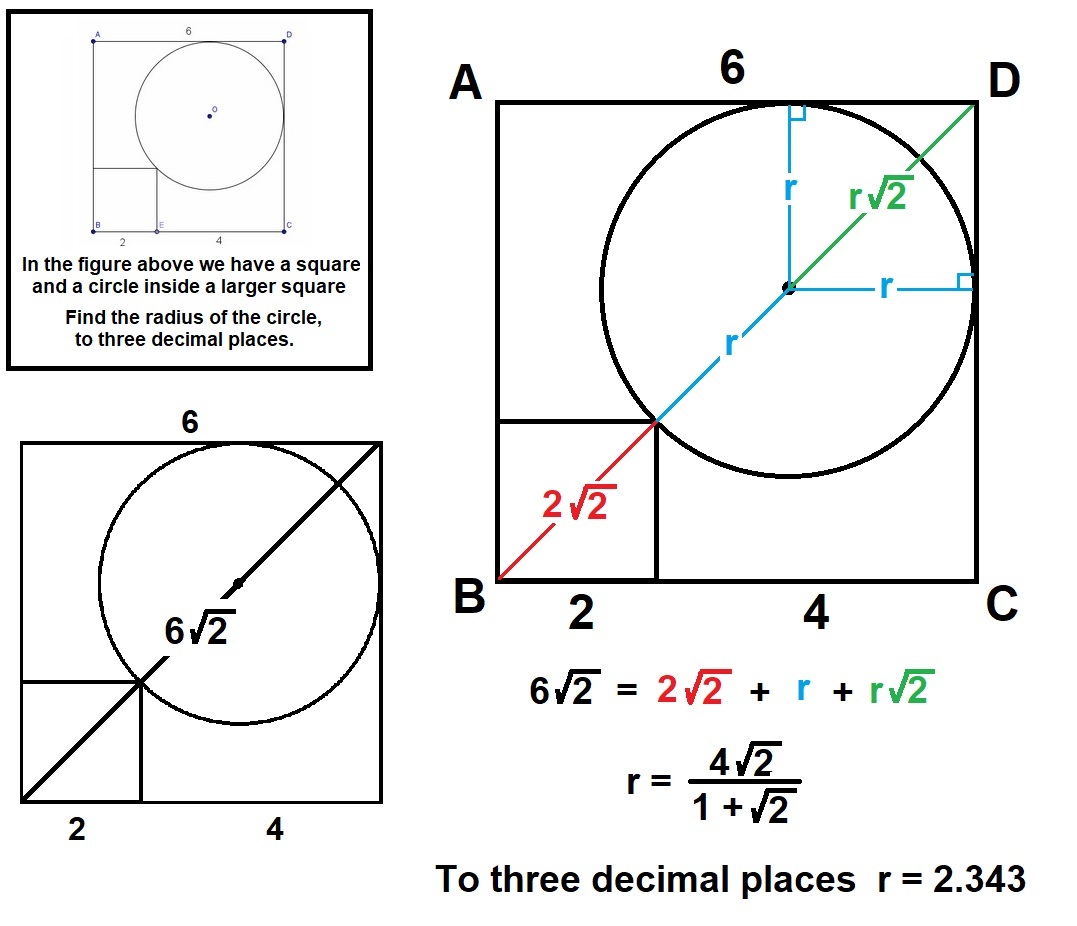
Square inside a square
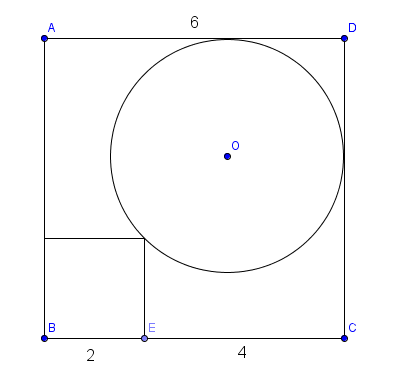 In the figure above, we have a square and a circle inside a larger square.
In the figure above, we have a square and a circle inside a larger square.
Find the radius of the circle, to 3 decimal places.
The answer is 2.343.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
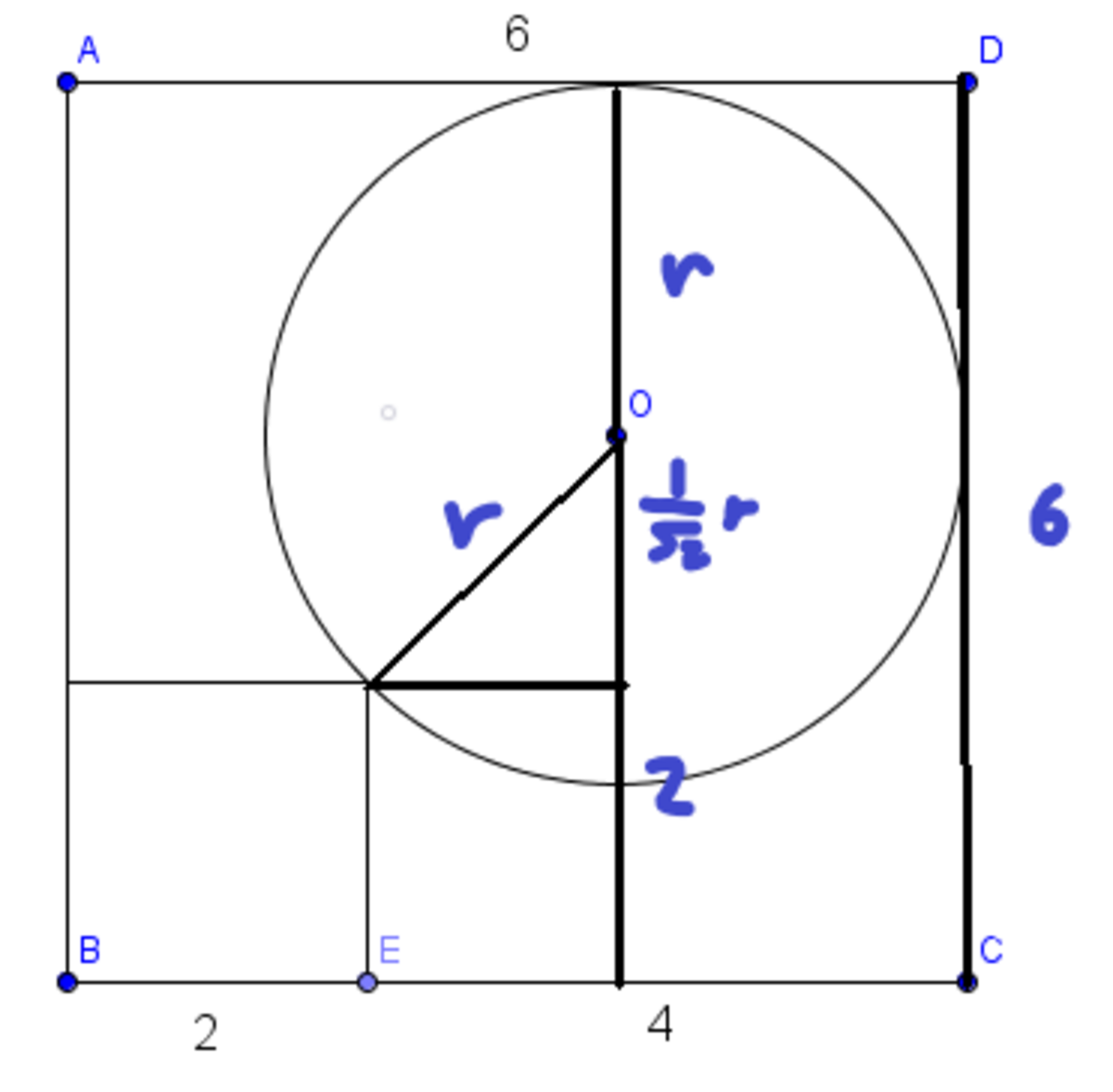
You can also do x + x s i n 4 5 ∘ = 4 and then solve for x . This will take you to the answer in 2 - 3 steps. (I have posted my solution for details).
Log in to reply
Used same approach though with cos, which is indeed the same when angle is 45 degrees. Seems more simple than first method.
Its cos. Not sin.
Log in to reply
It does not matter if angle is 4 5 ∘ .
It would be great, if you explain each step so that other may rationally understand each step, E.g. Why x + x + r = 4 (under root 2). Many kids would be pleased to have this question answered in detail.
Log in to reply
As the side of bigger square is 3 times the side of smaller square, the length of their diagonals will also be in the same proportion. Therefore, x + x + r = twice the diagonal of smaller square = 2 x( 2 root 2) = 4(under root 2).
Solved in the same way!!
How do we know that the diagonal passes through the center of the circle.
How do you know that the diagnol of small square is a part of diagnol of large squares and diameter? Please provide a proof of possible
Log in to reply
The diagonal is an axe of symmetry
The diagonal in this case is the angle bisector to the pair of perpendicular tangents to the circle. They always pass through the centre in any given case
Why in the world would you have a variable r that is not the radius? That seems really unintuitive
Where do you create these diagrams (because I was thinking of creating a geometry problem myself )?
Log in to reply
I create with GeoGebra
You can simply create in MS Word or MS Paint.
sala answer 2.5 hoga tum log galat hai
Log in to reply
Yes my answer is also 2.5
Log in to reply
If you are confident about your answer then post your solution.
bhai, 2.34383 barobar hai
btw writing in hindi isn't really gonna help the mexican read your response
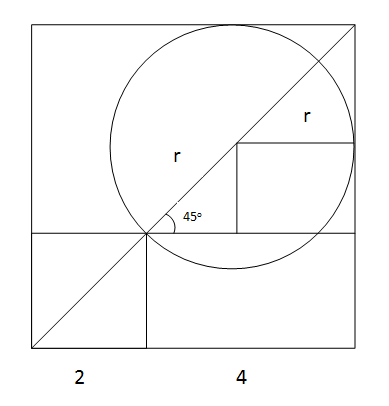
From the figure we see that r c o s 4 5 ∘ + r = 4
⟹ 2 r + r = 4
Solving this equation we would get r = 2 + 1 4 2 ≈ 2 . 3 4 3 u n i t s .
Ingenious!
Perfect!..I did the same..
how you got rcos45?
I used a trick and said that r = 4 - (4/(1+sqrt(2))) to get a more precise result, does it help the rounding ?
This was my way too.
Let the top and right sides of the square be the x and y axis respectively (in the third quadrant). Let the radius of the circle be "r". We can write an equation of the circle. The center is (-r,-r) because it is touching both axis in the third quadrant. The radius is r as we give it. Therefore, the equation is (x+r)^2 + (y+r)^2 = r^2.
Now we need to substitute in a value. As it touches the tip of that square, we can substitute in that value. On the co-ordinate plane, that is equivalent to (-4,-4). We then get the equation r^2 - 16r + 32 = 0. Solving, we get 8 - 4*sqrt(2) which is equivalent to 2.343.
Nice solution with coordinate geometry :)
Yes, I also think it's an ingenious way of solution. I thought of it but in the first quadrant, so it seemed complicate and I looked for another way. Taking the whole figure to the third quadrant is brilliant.
 r
+
2
1
r
+
2
=
6
r
+
2
1
r
+
2
=
6
r + 2 1 r = 4
2 1 + 2 r = 4
r = 2 + 1 4 2
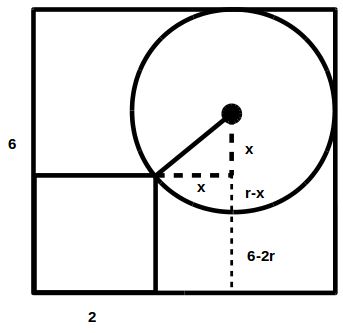 We get that
x
is
2
1
. So
2
=
(
6
−
2
r
)
+
(
r
−
2
r
)
, giving us
r
=
1
+
2
4
.
We get that
x
is
2
1
. So
2
=
(
6
−
2
r
)
+
(
r
−
2
r
)
, giving us
r
=
1
+
2
4
.
That does not calculate out to 2.343.. i dont believe your 1st statement is correct. Shouldn't it be r/(sqrt2)?
It needs to be r-(rsqrt2)/2... then it comes out right
Am I the only one who has used analitic geometry?
Hello @Luca Rossi also @FrEshy Pisuttisarun has used coordinate geometry
Placing the corner B at the origin of the x y − plane, the circle can be modeled as [ x − ( 6 − r ) ] 2 + [ y − ( 6 − r ) ] 2 = r 2 . The circle intersects the smaller square at ( x , y ) = ( 2 , 2 ) , which gives;
[ 2 − ( 6 − r ) ] 2 + [ 2 − ( 6 − r ) ] 2 = r 2 ;
or 2 ( r − 4 ) 2 = r 2 ;
or 2 ( r − 4 ) = ± r
or r = 2 ∓ 1 4 2 ;
or r = 4 2 ⋅ ( 2 ± 1 ) = 8 ± 4 2 .
Since the minus root makes physical sense for this nested configuration, the radius is just r = 8 − 4 2 ≈ 2 . 3 4 3 .
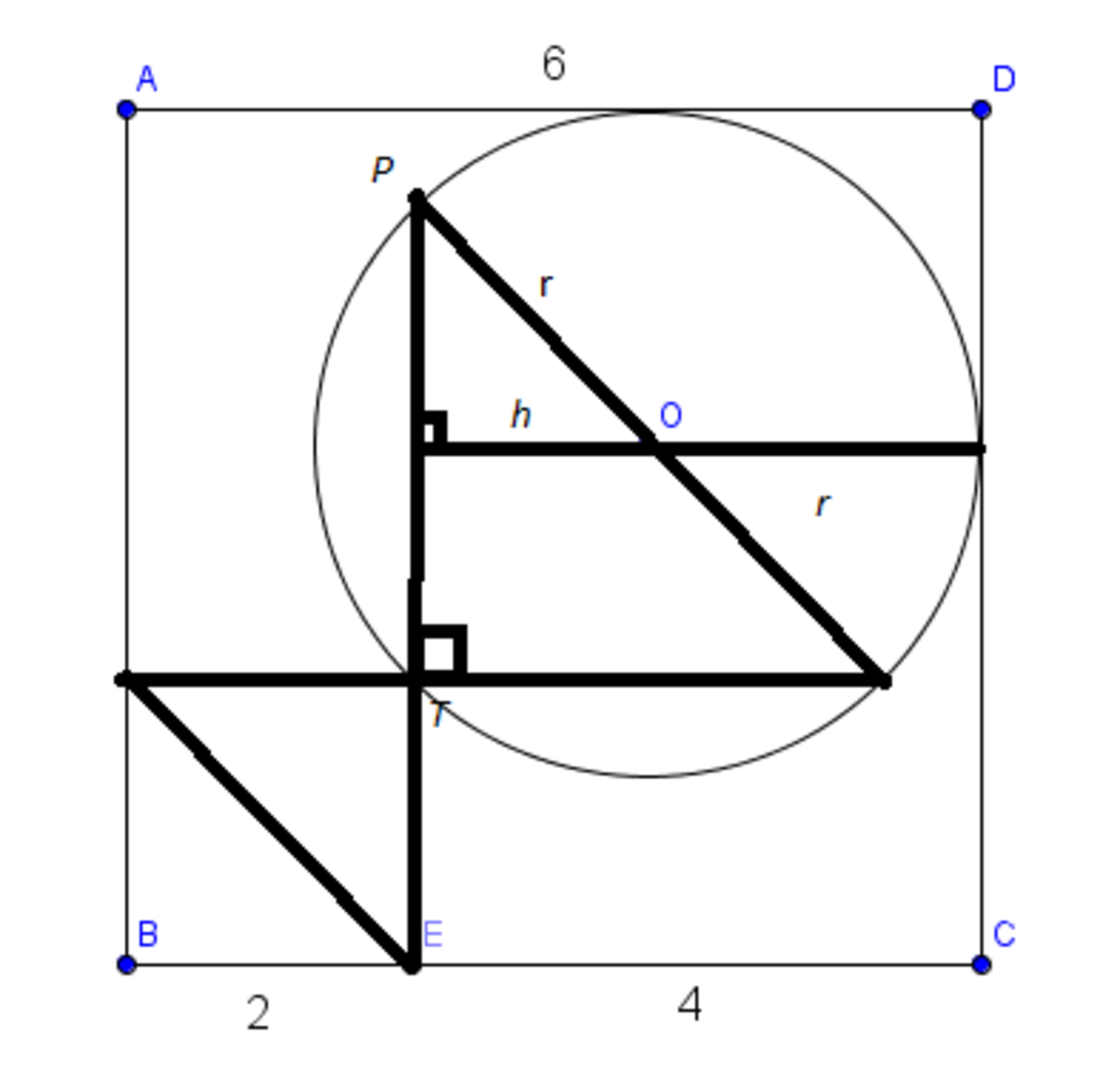
h + r = 4 .
2 2 2 r = 2 2 h
h = 2 r
⇒ r + 2 r = 4
r = 2 + 2 8 ≈ 2 . 3 4 3
I defined the distance from point O to line BC as x and the radius of the circle as r. Then using the length of one side: x = 6 - r. I then drew an isosceles right triangle in the bottom left of the large square. From the pythagorean theorem (x)^2 + (x)^2 = (r + 2*sqrt(2))^2. You can substitute 6-r into x in the equation above and then solve the resulting equation for r. Sorry I don't know how to use math formatting.
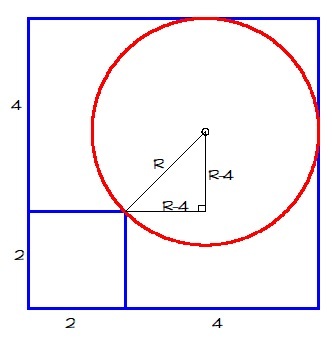 By the pythagorean theorem, we have
By the pythagorean theorem, we have
R 2 = ( R − 4 ) 2 + ( R − 4 ) 2
R 2 = R 2 − 8 R + 1 6 + R 2 − 8 R + 1 6
0 = R 2 − 1 6 R + 3 2
R = 4 ( 2 − 2 ) or R = 4 ( 2 + 2 )
The desired answer is R = 4 ( 2 − 2 ) ≈ 2 . 3 4 3 1 4 5 7 5 1
https://postimg.cc/WFThFtSw is this right
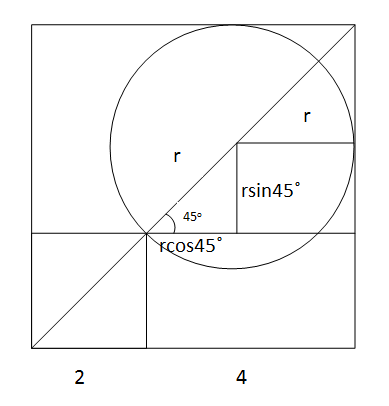

Let x the redius of the circle
x 2 = x + r so r = x 2 − x
Then
x + x + r = 4 2
2 x + x 2 − x = 4 2
x ( 2 + 1 ) = 4 2
x = 2 + 1 4 2 ≈ 2 . 3 4 3