Square Into Rectangles
A rectangle is cut from a unit square, and placed inside the remaining rectangle at an angle so that its 4 vertices touch the 4 sides of that rectangle.
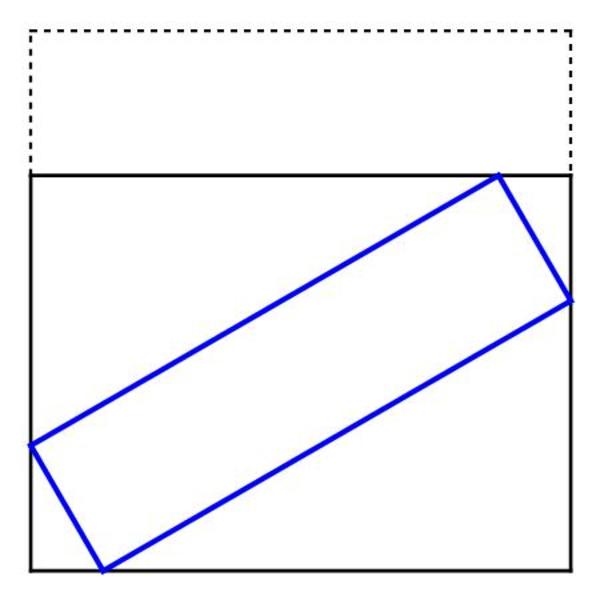
The width of the rectangle cut from the unit square can be expressed as a − b .
What is the sum a + b ?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Label the width of the rectangle x , the short leg of one of the large triangles y , and the other leg z . Since the four triangles are similar and a small triangle has a hypotenuse of x , its other legs are x y and x z .
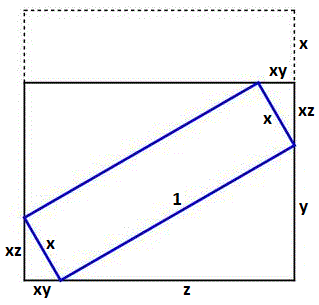
From the sides of the unit square, x + x z + y = 1 and x y + z = 1 , and by Pythagorean's Theorem, y 2 + z 2 = 1 .
These three equations solve to positive solutions of x = 2 − 3 , y = 2 1 , and z = 2 3 , so a = 2 , b = 3 , and a + b = 5 .
You used yz instead of xy in the diagram.
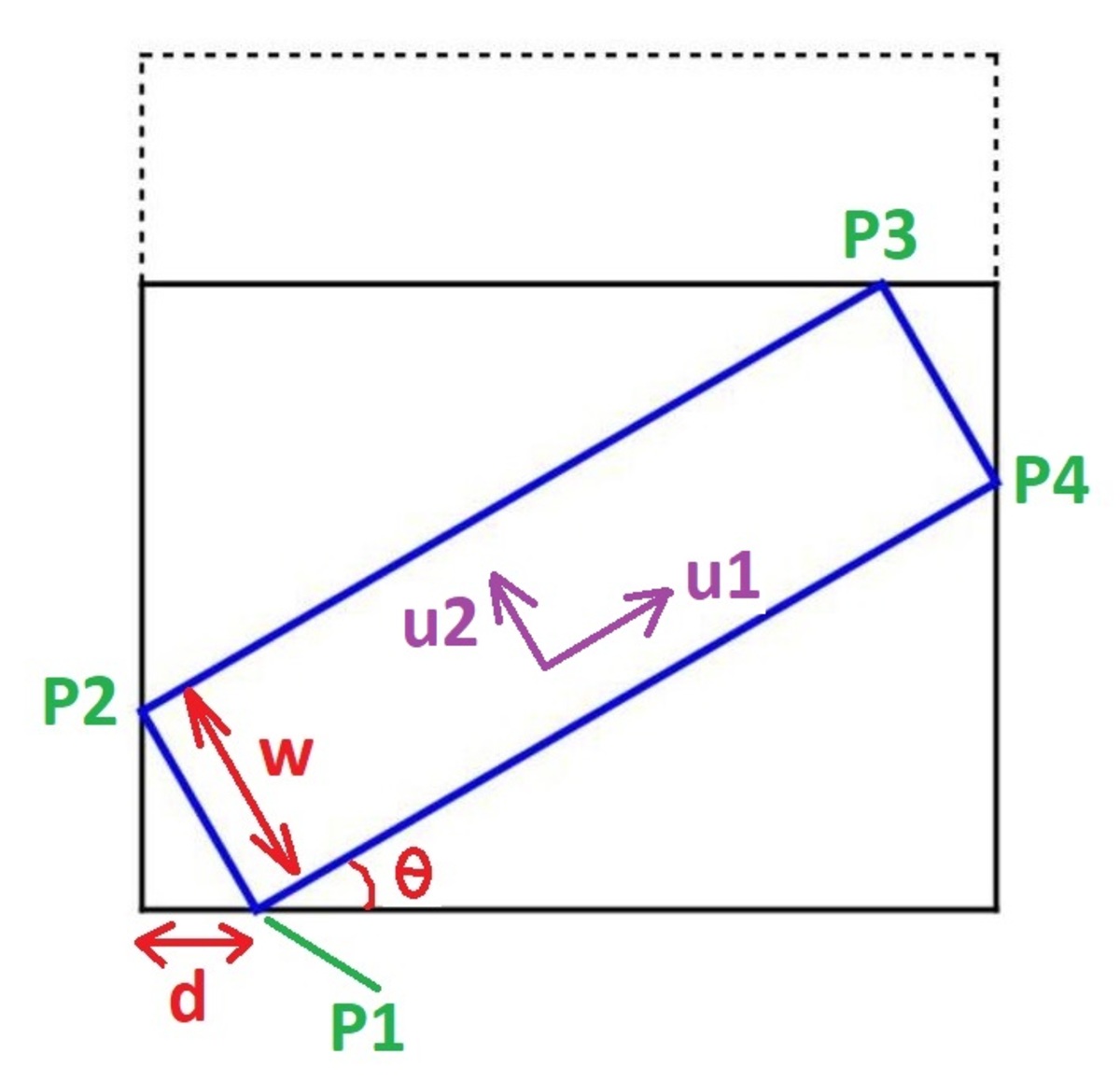
Let the lower left square corner be ( 0 , 0 ) .
Define some unit vectors:
u 1 x = cos θ u 1 y = sin θ u 2 x = − u 1 y u 2 y = u 1 x
These are the criteria for selecting parameters:
P 2 x = 0 P 4 x = 1 P 3 y = 1 − w
Fleshing these out:
d + w u 2 x = 0 d + u 1 x = 1 u 1 y + w u 2 y = 1 − w
Determine ( w , d , θ ) such that the above three equations are satisfied. I solved numerically, yielding:
w ≈ 0 . 2 6 7 9 5 ( 2 − 3 ) d ≈ 0 . 1 3 3 9 7 θ ≈ 3 0 ∘
What about limiting case of width =1/2 when rectangles overlap?
Divide length and width of square in x and y being small parts, setup equation for length and area conservation and solve for x & y.
y=2-√3
Answer=2+3=5
Let the width of the cut-out rectangle be x and the smallest angle between the two rectangles be θ as shown in the figure above. Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ x cos θ + sin θ = 1 − x x sin θ + cos θ = 1 ⟹ x = 1 + cos θ 1 − sin θ ⟹ x = sin θ 1 − cos θ
⟹ 1 + cos θ 1 − sin θ sin θ − sin 2 θ sin θ − 2 sin 2 θ sin θ ( 1 − 2 sin θ ) ⟹ sin θ ⟹ θ = sin θ 1 − cos θ = 1 − cos 2 θ = sin 2 θ = 0 = 0 = 2 1 = 6 π Since θ > 0
Therefore x = 2 1 1 − 2 3 = 2 − 3 and a + b = 2 + 3 = 5 .