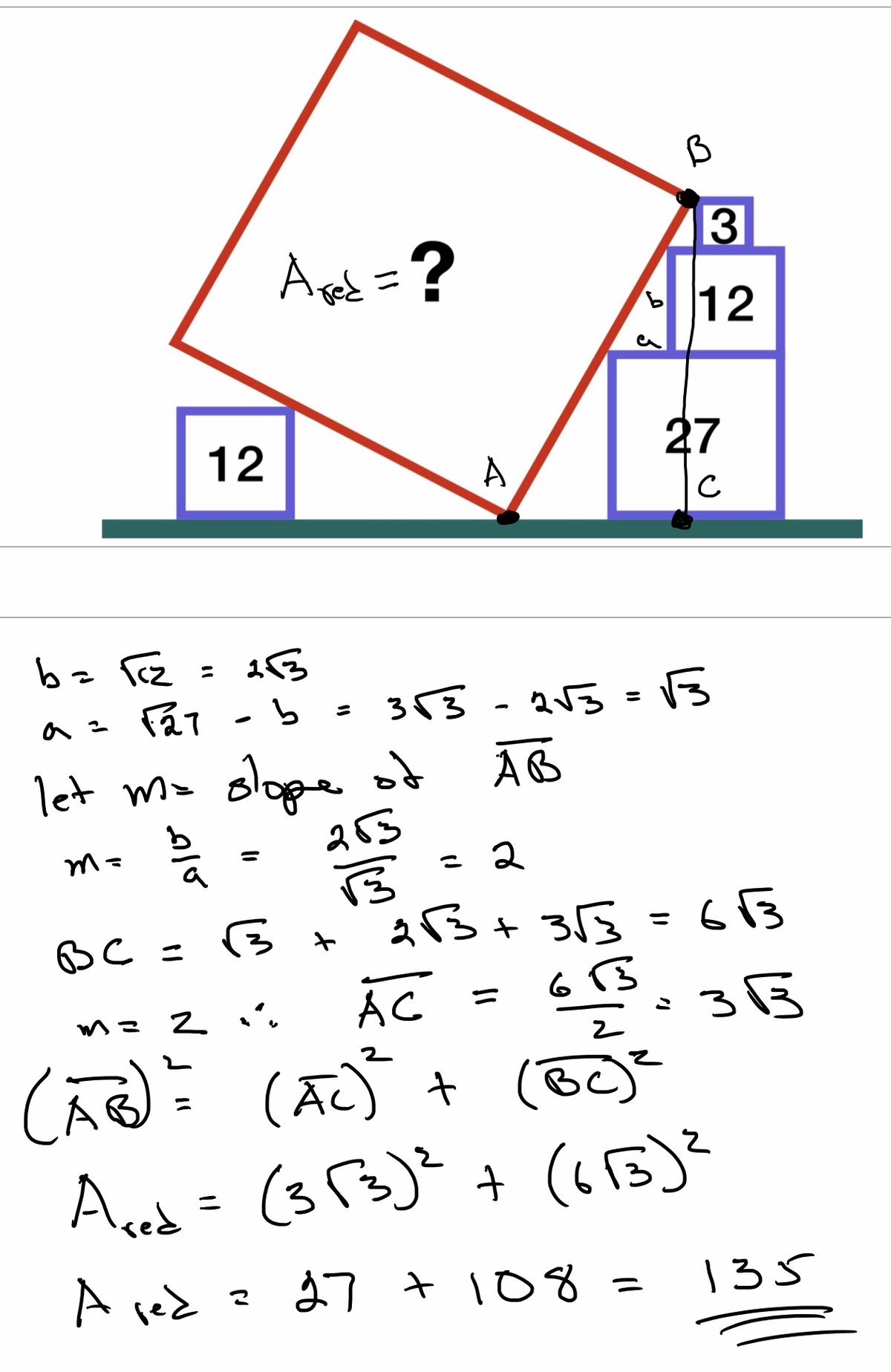
Square knocked down

We note that the three grey right triangles in the figure are similar. The side lengths of the three squares on the right are $\sqrt 3$ , $\sqrt {12}= 2\sqrt 3$ , and $\sqrt{27}= 3\sqrt 3$ . Therefore, the ratio of side lengths of the three similar grey right triangles is $1:2:3$ .

Let the base length of the middle grey right triangle be $a$ and its hypotenuse be $b$ . Assuming the right edges of the $2\sqrt 3$ -square and $3\sqrt 3$ -square are aligned, then $a=3\sqrt 3- 2\sqrt 3=\sqrt 3$ . By Pythagorean theorem, we have $b^2 = a^2 + (2\sqrt 3)^2 = 3+12 = 15$ $\implies b = \sqrt{15}$ .

Let the side length of the large square be $s$ . Since the ratio of side lengths of the three similar grey right triangles is $1:2:3$ , $s=\frac {1+2+3}2b = 3b = 3\sqrt{15}$ and the area of the large square $A=s^2 = (3\sqrt{15})^2 = \boxed{135}$ .

Since $\gcd (3,12,27) = 3$ , the area ratio $3:12:27$ is equivalent to $1:4:9$ , which transforms the given diagram to the following:

Figure 1. Diagrams with primitive areas

Since the segments of the square are linear and perpendicular, the purple squares can be produced as shown:

Figure 2. Lines extended to form purple squares; notice that the largest blue square extends outward and also shares the common vertex with the red square. Thereby, geometry easily shows that the lengths of the largest inner triangles are 3 and 6. Computation verifies that there is no other possible setup with different solutions, which follows similarity of triangles.

where the stack of 3 small squares can be shifted to position two smallest squares inside the largest rectangle. In this case, the result follows the area of the tangential square in the largest square of side length $6+ 3 = 9$ :

Figure 3. Resulting diagram from Figure 1

where the area of the inner square is $45$ . Thus, $\dfrac{\text{Area of smallest blue square}}{\text{Area of red square}} = \dfrac{1}{45} = \dfrac{3}{135}$

which shows that the answer for this problem is $\boxed{135}$ .

Relevant wiki: Pythagorean Theorem

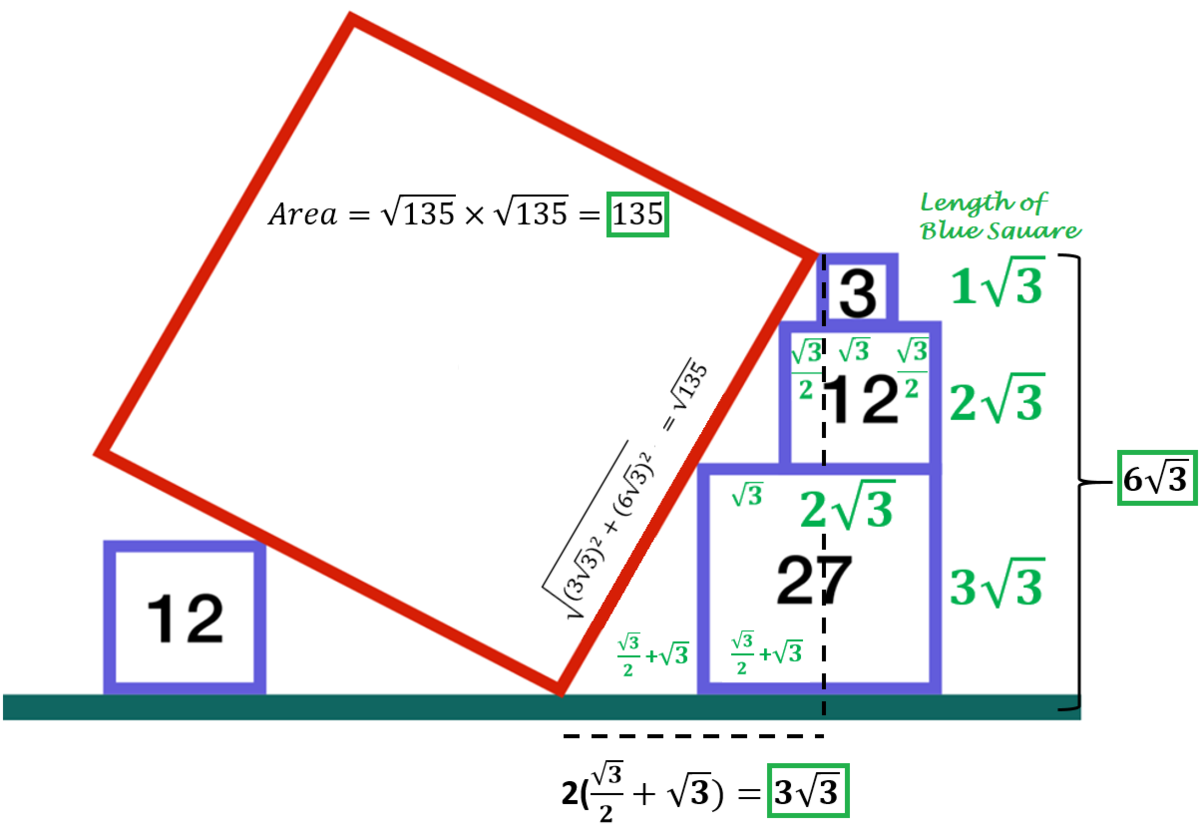In the right hand side of the image, the area of blue square equal to 3, 12, and 27 and their corresponding side length equal to $\sqrt{3}, 2\sqrt{3},\ and \ 3\sqrt{3}$ respectively. Clearly, sum of the sides of the blue square equal to $6\sqrt{3}$ which is equal to black dotted vertical line .

The blue square with side length of $1\sqrt{3}$ placed in the middle of the blue square with side length $2\sqrt{3}$ . Difference of sides equal to $2\sqrt{3}$ - $1\sqrt{3}$ equal to $1\sqrt{3}$ . The length splitted as $\frac{(\sqrt{3})}{2}$ , $\sqrt{3}$ , and $\frac{(\sqrt{3})}{2}$ . Similarly, The blue square with side length of $2\sqrt{3}$ placed top of blue square with side length $3\sqrt{3}$ . Difference of sides equal to $3\sqrt{3}$ - $2\sqrt{3}$ equal to $1\sqrt{3}$ . The length splitted as $\sqrt{3}$ , and $2\sqrt{3}$ . The length of the black dotted horizontal line is $2(\frac{(\sqrt{3})}{2}$ + $\sqrt{3}$ ) equal to $3\sqrt{3}$ .

Using Pythagorean theorem, the length of red square is $\sqrt{135}$ , which is calculated using doted legs. Hence the area of the red square equal to $\sqrt{135}$ x $\sqrt{135}$ =135.

[(√27 - √12)/√12] = (1/2) gives the cot(x) of the angle, where "x" is the inclination of the right side of the red square. Therefore, the red square area

= {(√3+√12+√27)^2}(1+cot(x)^2)

Answer=135

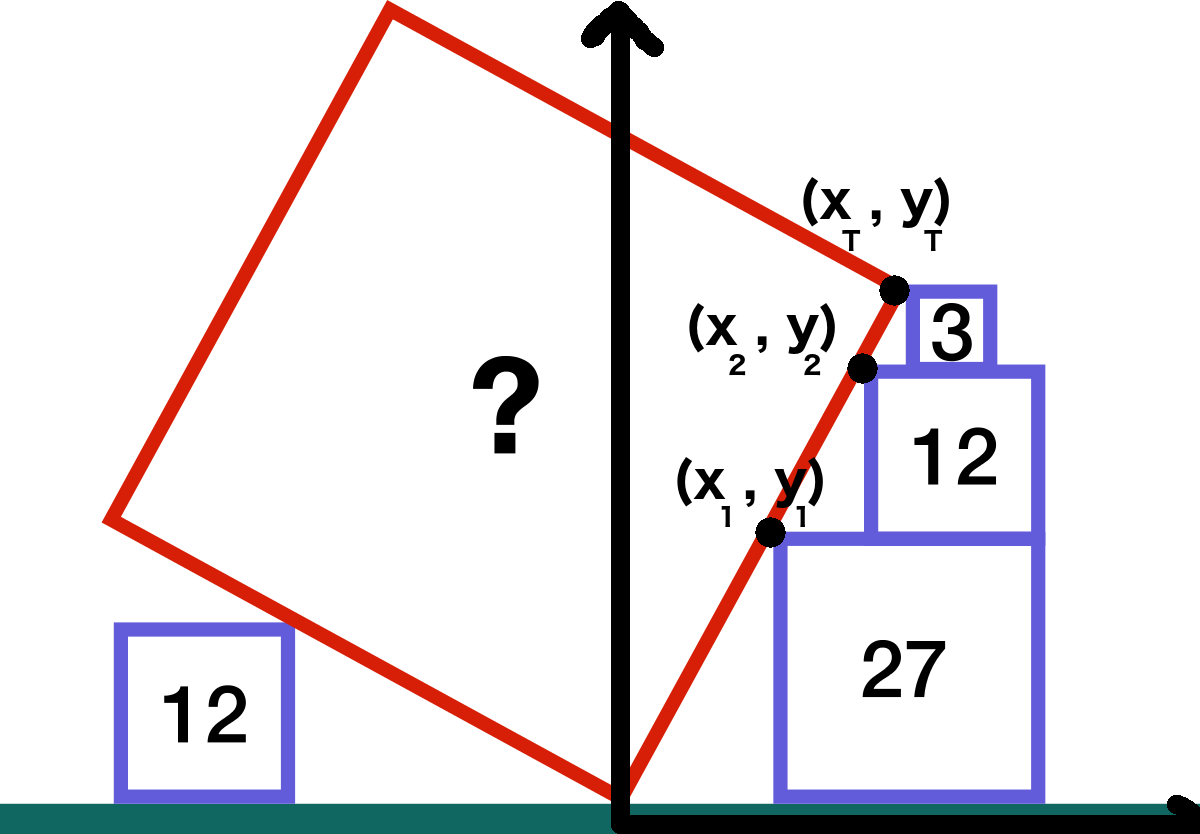We can solve the problem algebraically

From the diagram we know that $Y_{T}$ = $3 \sqrt{3}+2\sqrt{3}+\sqrt{3}=6\sqrt{3}$

To find $X_{T}$ we need to find the slope of the line

Slope = $\frac{\Delta Y}{\Delta X}$ = $\frac{Y_{2}-Y_{1}}{X_{2}-X_{1}}$ = $\frac{2\sqrt{3}}{3 \sqrt{3}-2\sqrt{3}}$ = $\frac{2\sqrt{3}}{\sqrt{3}}$ = 2

note: $\Delta X$ is the difference between the length of the side of the bottom square and the length of the side of the middle square and $\Delta Y$ is the length of the side of the middle square

Therefore $X_{T}$ = $\frac{ Y_{T} }{Slope}$ = $\frac{6\sqrt{3}}{2}$ = $3 \sqrt{3}$

Area = $Side^{2}$

Area= $Side^{2}$ = $Y_{T}^{2}$ + $X_{T}^{2}$

Area= $(6 \sqrt{3})^{2}$ + $(3 \sqrt{3})^{2}$

Area= $\boxed{135}$

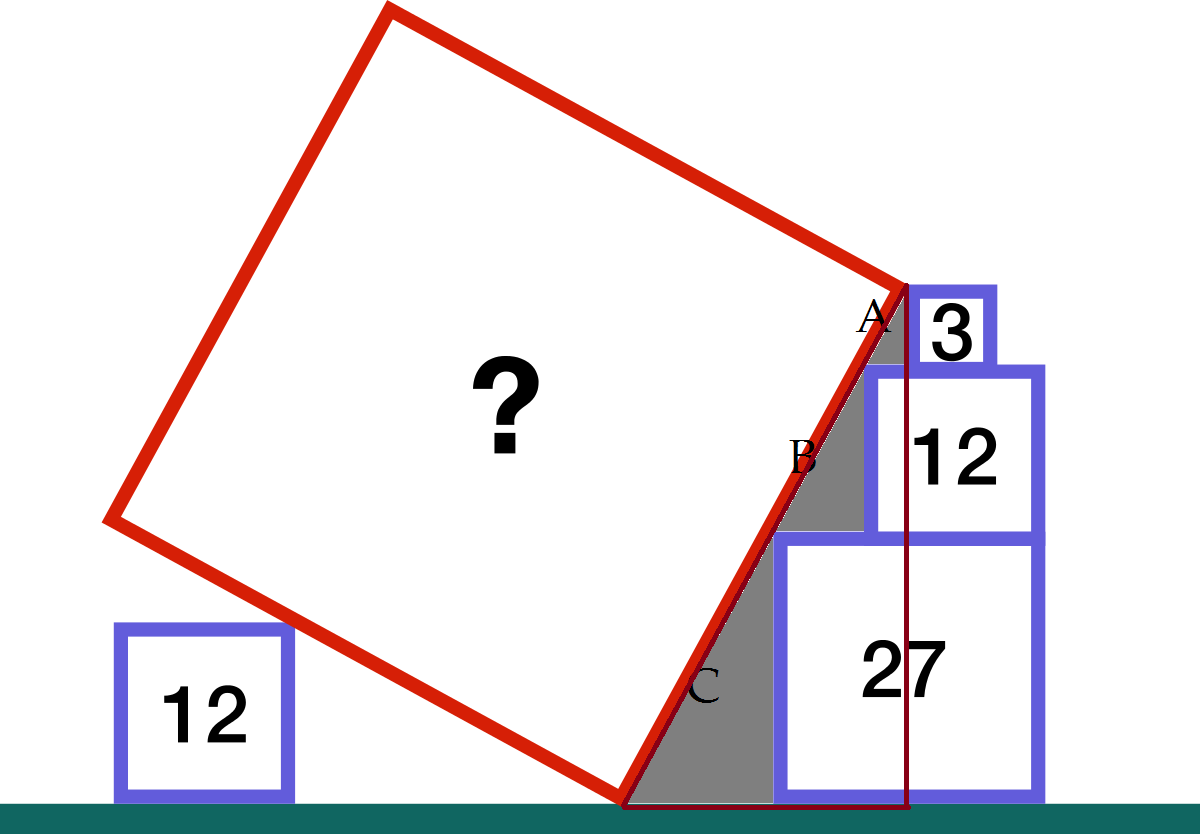
Similar triangles are the key! Let the triangles A,B,C be the three similar grey triangles marked in the picture. We know they are similar because the angle the red square's side makes with the blue squares' side is the same, and the angle opposite to the red square's side is always 90 degrees.

Notice that the heights of these triangles are $\sqrt{3}$ , $2\sqrt{3}$ and $3\sqrt{3}$ , respectively, implying that the three of them are such that C is three times as large as A, and B is twice as large as A. Moving on, notice that the lower-right vertex of the 12 square coincides with the upper-right vertex of the 27 square, implying that the base of triangle B is $\sqrt{27}-\sqrt{12}=\sqrt{3}$ , which, in turn, implies the base of triangle A is $\frac{\sqrt{3}}{2}$ and the base of triangle C is $3\frac{\sqrt{3}}{2}$ .

Let's now turn our attention to the triangle marked in red. Notice that its height equals the sum of the side lengths of the 3, 12 and 27 squares, totaling $6\sqrt{3}$ , and its base is the sum of the side lengths of A,B, and C, totaling $3\sqrt{3}$ . We then apply pythagoras:

$(6\sqrt{3})^2+(3\sqrt{3})^2=l^2=135$ where l is the side length of the red square, implying its area is 135.

Woops, forgot the picture:

Consider: 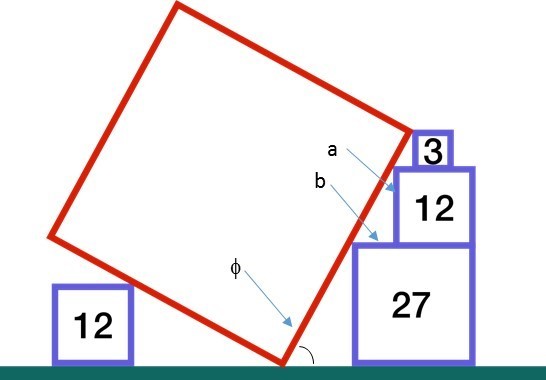Assume that the 12 and 27 squares are right aligned. Tan (phi) = a / b = sqrt(12)/[sqrt(27)-sqrt(12)] = 2

Now consider: 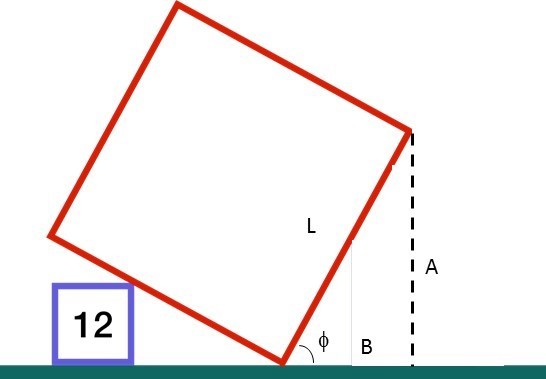Area = L^2 = A^2 + B^2. From the above, A/B = 2, so Area = 5/4 A^2

A = sqrt(3) + sqrt(12) + sqrt(27)