Square numbers in squares
Peter placed the numbers
in the figure, so that each square contained exactly one number. Suddenly, his cat jumped on his table, knocking over his tea and six numbers disappeared (as shown in the figure).
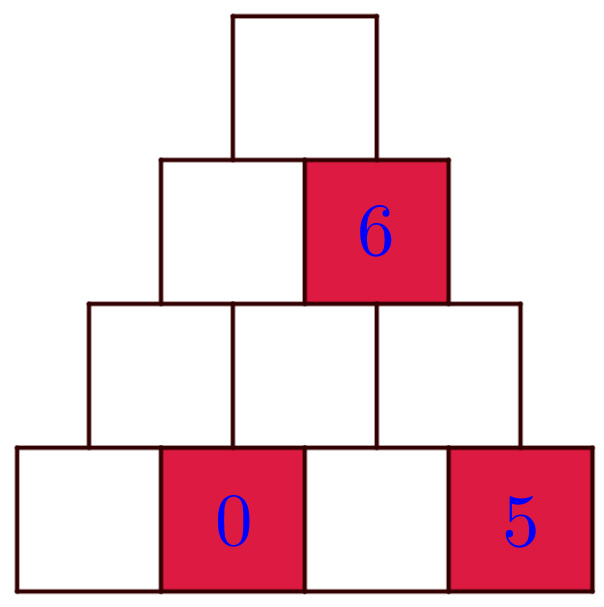
In how many ways could he have placed the numbers, if by reading the numbers (from left) in each row we get a square number?
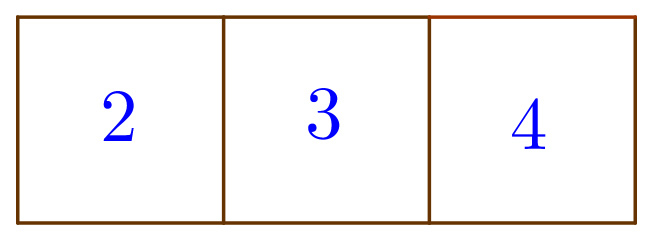
So for example if we place the numbers in the third row in the figure above, then the number would have to be a square number.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
a = v 2
b 6 = x 2
c d e = y 2
f 0 g 5 = z 2
Since 5 ∣ z 2 , 5 ∣ z , but z is not a multiply of 1 0 . So z has 1 0 possible values: 5 , 1 5 , 2 5 , … , 9 5 . From these the 5 5 2 and 9 5 2 could be f 0 g 5 .
If f 0 g 5 = 3 0 2 5 , then x has only one possible value: x = 4 and b 6 = 1 6 . A square number's possible endings: 0 , 1 , 4 , 5 , 6 , 9 , so a and e are 4 and 9 in a way. If a = 4 , then c d e would be 7 8 9 or 8 7 9 , but non of these is a square number. So a = 9 and c d e only could be 7 8 4 . So if f 0 g 5 = 3 0 2 5 , then there are one possible placing.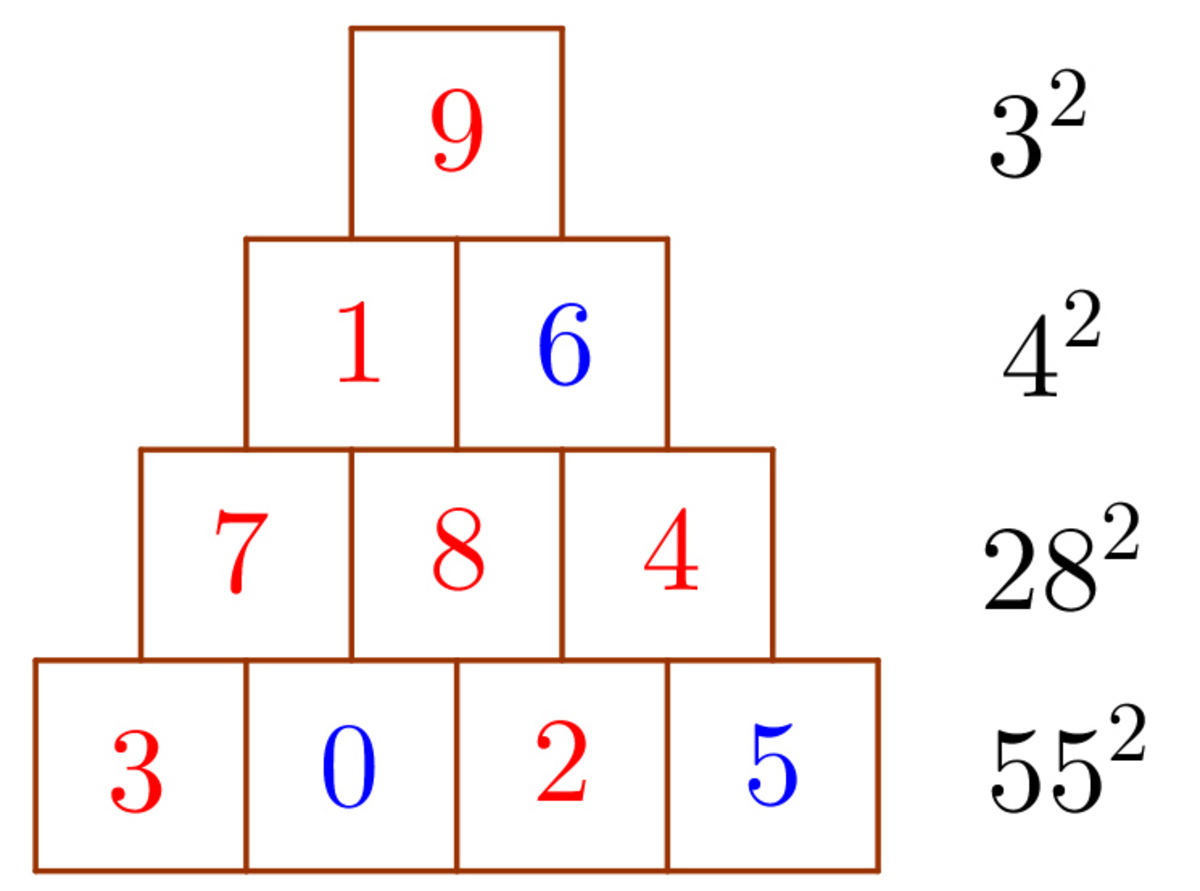 If
=
9
0
2
5
, then
b
6
only can be
3
6
, because if it would be
1
6
, then from the
3
,
4
,
7
,
8
digits we would have to make two square numbers, but square numbers' endings are from the
0
,
1
,
4
,
5
,
6
,
9
digits. So because neither
7
8
4
nor
8
7
4
is a square number,
a
=
1
, and because
8
7
4
is not a square number,
c
d
e
=
7
8
4
.
If
=
9
0
2
5
, then
b
6
only can be
3
6
, because if it would be
1
6
, then from the
3
,
4
,
7
,
8
digits we would have to make two square numbers, but square numbers' endings are from the
0
,
1
,
4
,
5
,
6
,
9
digits. So because neither
7
8
4
nor
8
7
4
is a square number,
a
=
1
, and because
8
7
4
is not a square number,
c
d
e
=
7
8
4
.
So there are two possible numbering.