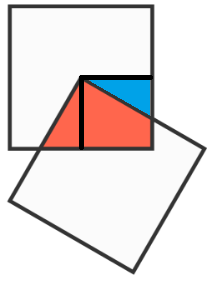
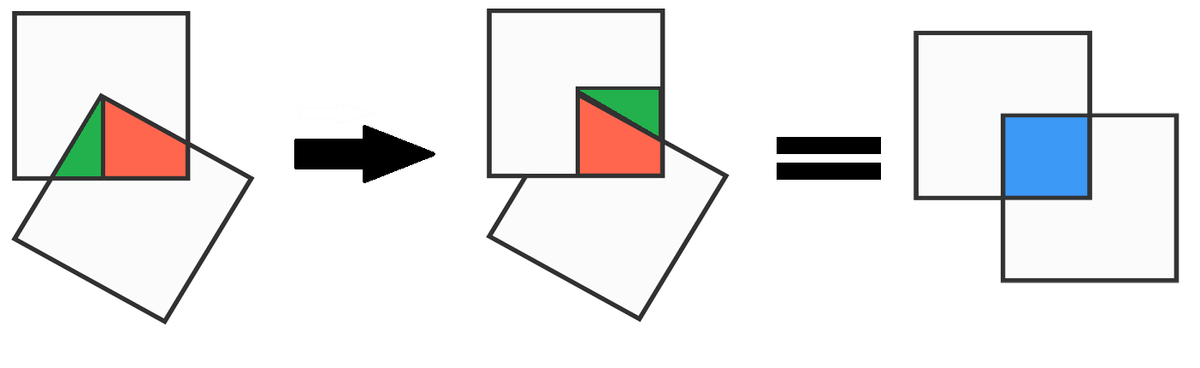
Square on top of another
A vertex of one square is pegged to the center of an identical square, and the overlapping area is blue. One of the squares is then rotated about the vertex and the resulting overlap is red.
Which area is greater?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
30 solutions
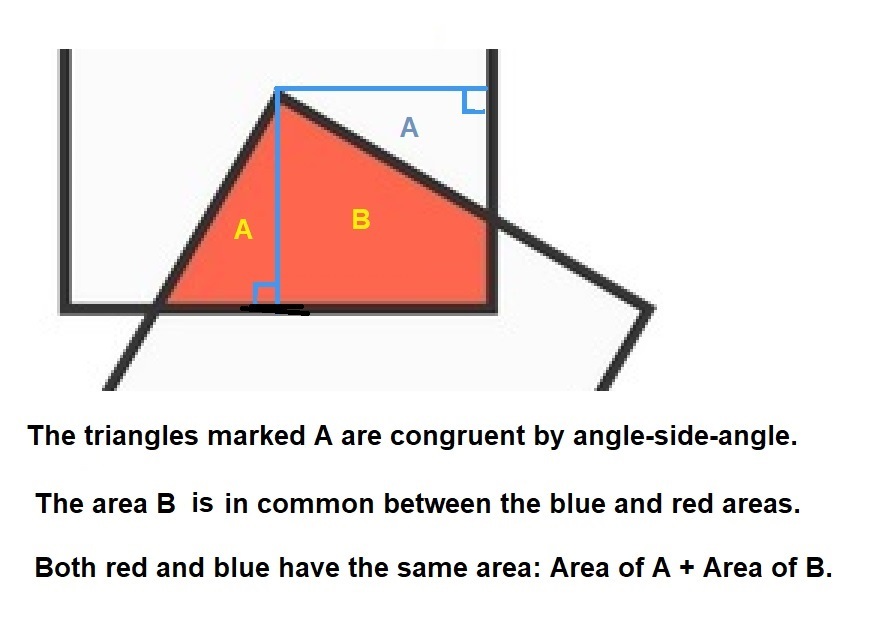
“ASA”, so they are congruent.
So razor-sharp-ly said!
That's a simple rotation isometry, no?
this is a smart and true way of solving this question
No matter how much you rotate the square, it will always be 1/4 of the square that is overlapped.
May i know how
Log in to reply
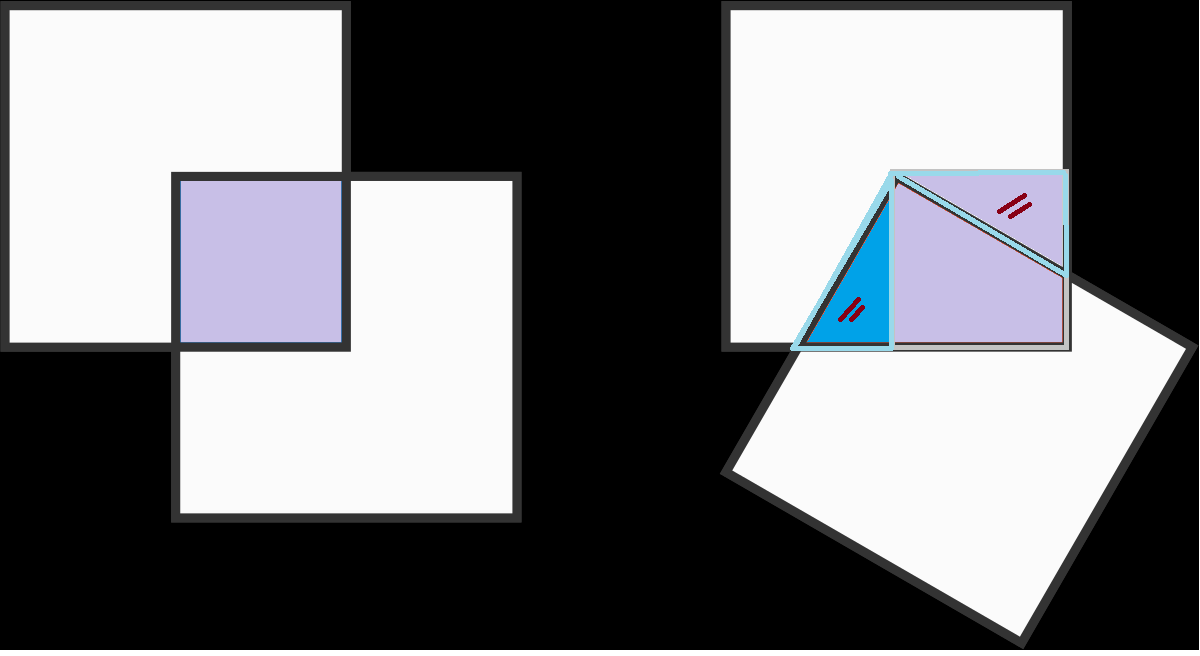
Consider using 4 squares pinned to the center of the starting square to that the entire original square is covered. Each "new" square covers 1/4 of the original. When they rotate, by symmetry the areas covered by each are still equal and together they cover the whole thing, so... still 1/4.
Log in to reply
That's very similar to the way I looked at the question. Great observation!
Yeah i agree only 1/4 will be overlapped
I drew the same conclusion but from intuition. I need to think through it some more to be able to explain it.
It depends where you put the vertex doesn't it? if you have the vertex about middle height, but well to the right of the square, the blue area becomes a long thing rectangle, but when you rotate it, the red are will become bigger than the blue.
Log in to reply
Doesn’t the question state the vertex of one square is in the centre of the other?
Log in to reply
Yes, “The vertex of one square is pegged to the exact center of an identical square.” Elegant solution!
What’s the point of discussing something outside of the current problem?
This is just restating the question , it does not answer it. You need to prove that it is always the same amount overlapped.
I thought that since the base of the red rotated square was bigger and the height was the same, The red shape would be bigger, to do this, I I just drew them out on a piece of paper and then I measured them. I don't really get how 1/4 of the square is always overlapping though. I would rate this problem a 6 because it was kind of confusing and I don't really get it. I felt a little confused at why the answer was wrong.
What you’re giving is the answer and not a solution.
As given if the vertex of second square is pinned at the center. And suppose if the side of the square is : X unit. Then it will always form 2 right angle triangle of sides : X unit, X-y unit. i.e: (X, X-y) and (X, X-z) Where z, y will lie between : 0 < z, y < X. thus just by changing the z, y value you can rotate the other square at any degree.
Try to visualize it you'll understand.
Without considering the geometry of the enclosed area, I visualize the perimeter as remaining unchanged as the bottom square is rotated. It follows then that the enclosed area remains unchanged as well.
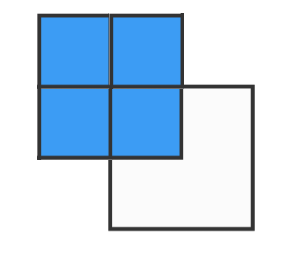
For me it was easier to see that the area of the square is made of 4 little blue squares but also 4 red shapes
area square = 4 x blue square
area square = 4 x red shapes
=> the area of the blue square and the red shape are equal
i learned and get it
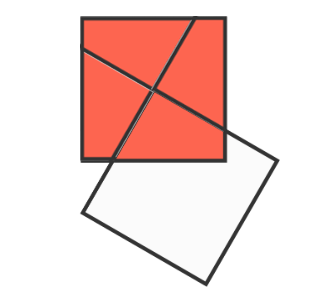
 It is true for any regular polygon - the area of intersaction is constant for any angle of rotation.
It is true for any regular polygon - the area of intersaction is constant for any angle of rotation.
Thanks for generalizing. +)
When the vertex is fixed the area will be equal
Thanks for generalising.
A simple way to think about it is to rotate the second square a little further to 45 degrees to make a red triangle. You can clearly see that it still makes up a quarter of the square's area (squarea?).
Taking the side of the square = 2
x + y = 2
x = 2 - y
a = y + (1 - y)/2 + (x -1)/2
a = y + 1/2 -y/2 + x/2 - 1/2
a = y - y/2 + (2 - y)/2
a = y - y/2 + 1 - y/2
a = 1
i don’t get it ^
I see it as three points. One is fixed and the others traverse on a defined locus (the perimeter of fixed square). The area swept will always be the same.
Put 4 identical squares pegged to the center of the square instead of only one. Then rotate them all the same quantity about the vertex. The overlapping are of each of them with the center square is obviously the same and their sums a the area of the wole square so the will remind the same 1/4 no matter how much you rotate them. It is another way to look at the solution.
very nice solution! I also thinked it that way :)
No matter what degree will you rotate it, it will always be the same in AREA if any of the figure will rotate about a fix point.
Since squares are symmetrical, if you added a remaining three squares pinned to the centre of the centre square, no matter which way you rotated them, they could only ever have a equal portion each, which therefore must be one quarter.
Consider four overlapping squares, each with a corner at the vertex. They all overlap the entire area of the central square, with equal amounts at the corners as shown in the first picture, and also when they create four equilateral triangles when rotated through forty five degrees. To overlap a different amount at some intermediate angle of rotation would require the overlap of one square to increase or decrease, which would be opposite for an adjacent square, yet the position of each of the four squares would be identical, so the overlap can’t change and must at all positions be the same, and be quarter of the area of any overlapped square (regardless of its size).
Regardless of the rotation of the "2nd" square, it will always cover 1/4 of the area of the "1st" square
By making the square rotate we can only change the shape of overlapping surface but if the vertex of square is exactly at center of other square it doesn't affect the area..
Cover the entire square by four identical copies of the overlapping square. Then in the left picture each subsquare covers an equal amount, and will by symmetry/congruency continue to do so under arbitrary rotations of the quadruple square. Because the quadruple square always covers the entire square during a full turn, each subsquare will consistently cover 1/4 which is evidently the cover in the left picture.
Basically when you rotate the square around, its just that some parts of a square are moved to the other
No matter the amount of angle rotated, it will consume an equal amount of area.
For me the easiest way to understand this is to imagine 4 squares covering the first square.
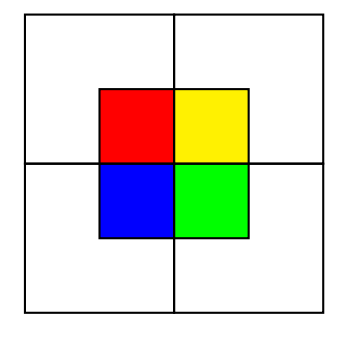
Even if you rotate them around, by symmetry, each square always covers one-quarter of the initial square.
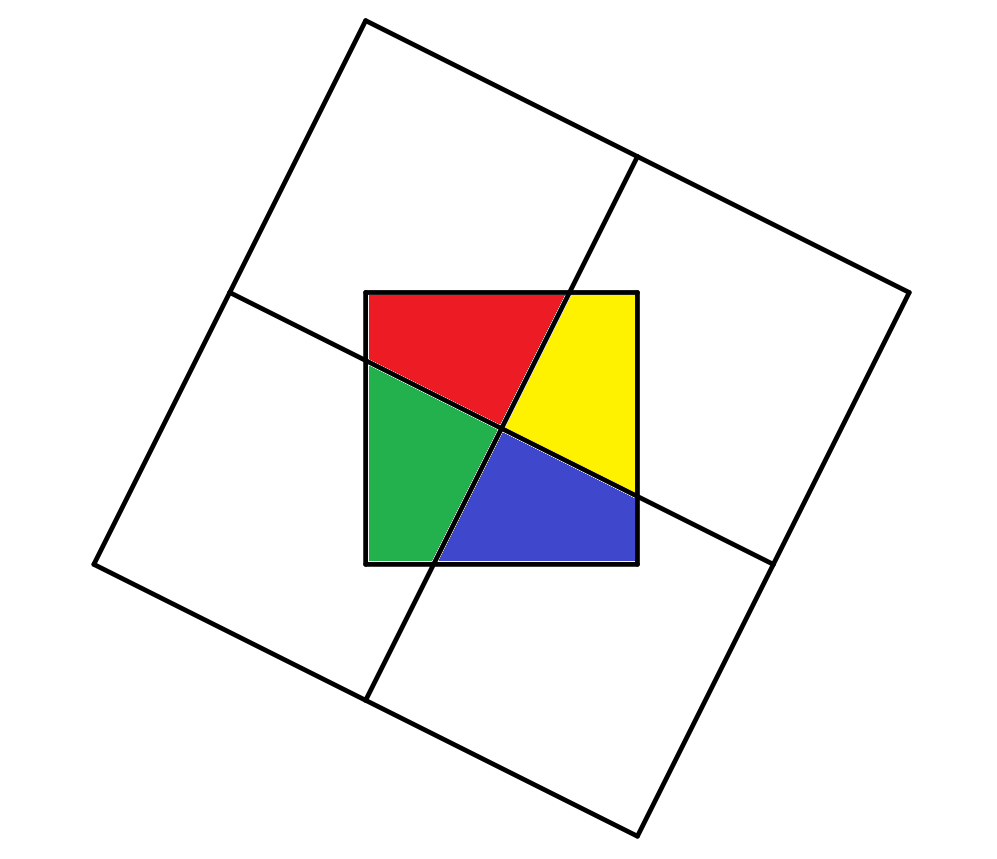
Therefore the area is always constant.
The way I saw it very quickly was that as the overlap with the vertical (A) line shrinks, the overlap with the horizontal (B) line grows. Just like matter can't be created or destroyed, this overlap can't grow or shrink, because the length of each line consisting of the overlap isn't shrinking or growing as a whole! By "as a whole" I mean that if overlap with one line shrinks, it will grow by the same amount elsewhere!!
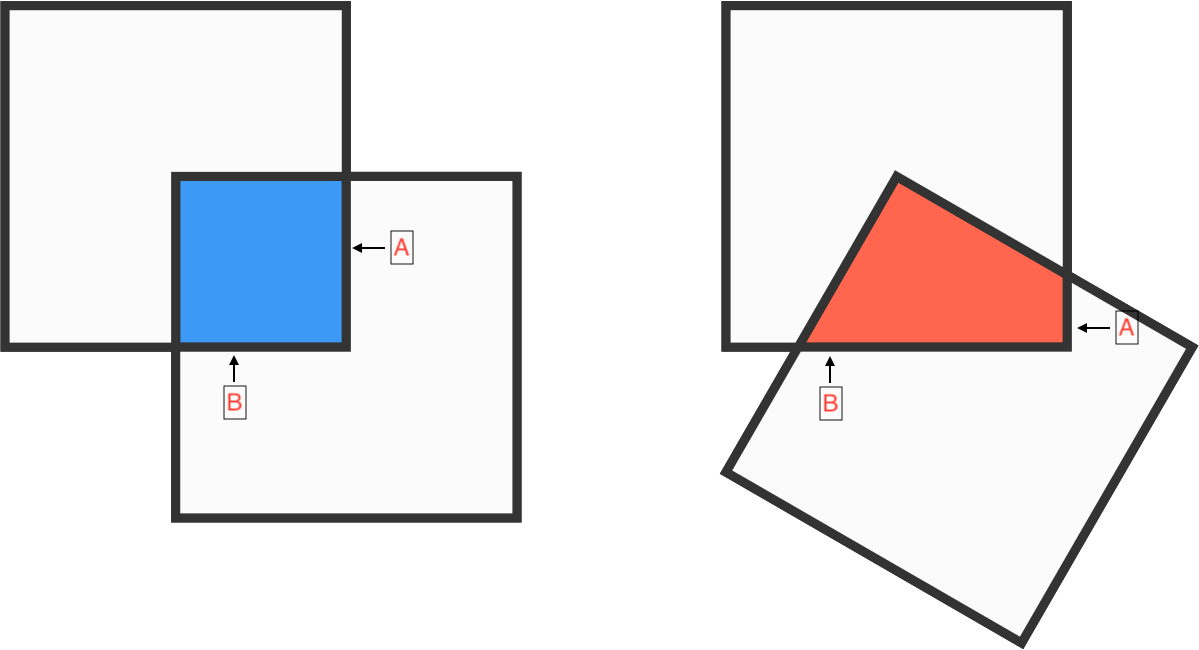
Simply this: If you take away a small slice by rotation, the same slice is gained on the other side. This implies the same property for all areas of rotation with similar parameters (angles of shape are all identical, shapes are identical)
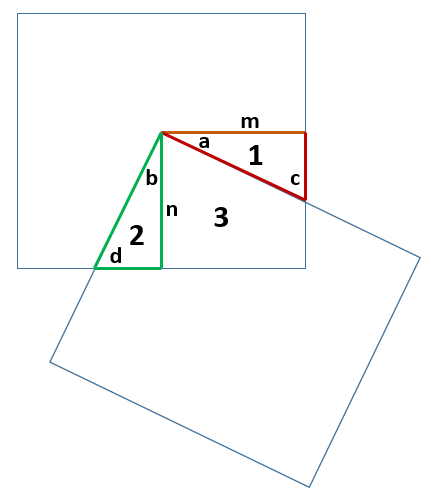
The triangles 1 and 2 are congruent (identical) because (1) two angles a=b and c=d; (2) one edge m=n. Therefore, the area 1+3 = 2+3.
If we draw a circle with half the length of second square from where the square is rotated,we get the same area in 2nd figure,as the length again remains the same.
The region that is in the rotated part, but not in the original square is equal to the part that is in the original square, but not in the rotated part. Therefore, they have equal areas.
Initial Area = l^2 Final Area = l^2 - (1/2) (l^2) tanx + (1/2) (l^2) tanx Where x is the angle by which the lower square is rotated around the centre.
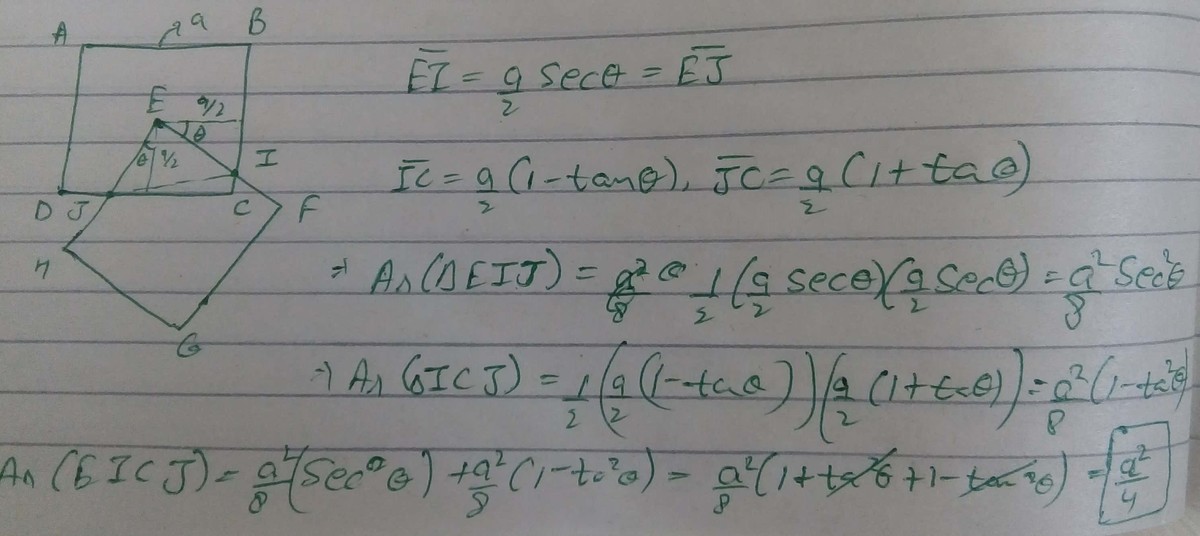
Relevant wiki: Basic Composite Figures
When the square is rotated about the vertex, the following red and blue triangles are congruent, and so the red triangle can move to the blue triangle's position, which means the red area is equal to the blue area.