Square plate

We'll assume that the plate is rotating with respect to B.

We have: $\vec{a_A} = \vec{a_B} + \vec{a_n} + \vec{a_t}$

Where $\vec{a_n}$ is the centripetal acceleration of A and $\vec{a_t}$ is the tangentical acceleration of A :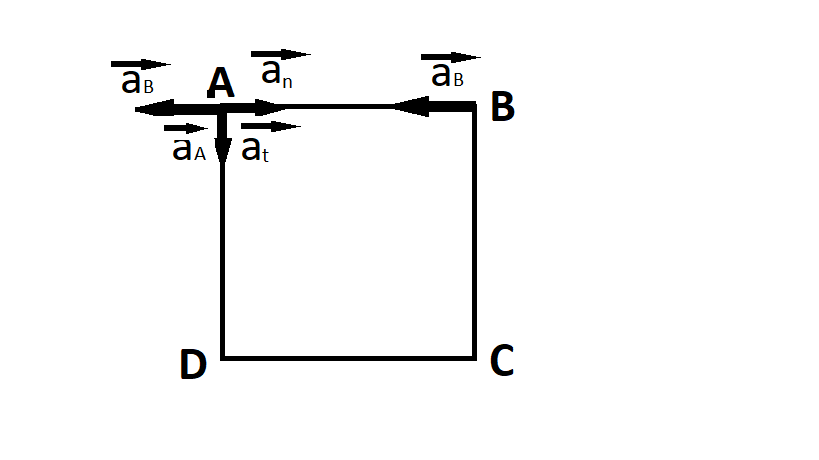

And so from the figure we can find that:

${a_n} = {a_B} = {a}$ => $\omega^2 * AB = {a}$ (centripetal acceleration formula)

${a_t} = {a_A} = {a}$ => $\gamma * AB = {a}$ => $\gamma = \frac{a}{AB}$ (linear and angular acceleration relationship).

From that we can find the rotating direction of our plate.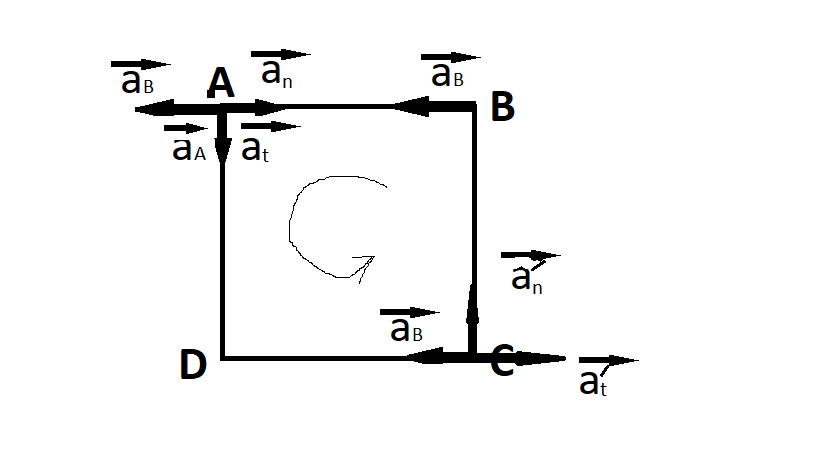

With the rotating direction given, we can determine the direction of the accelerations of C.

For point C we also have: $\vec{a_C} = \vec{a_B} + \vec{a'_n} + \vec{a'_t}$

With ${a'_n} = \omega^2 * BC = \frac{a}{BC} * BC = a$ and ${a'_t} = \gamma * BC = a$

And so we have ${a_C} = {a'_n} = a = 16 cm/s^2$