Right Square Pyramid with a special base.
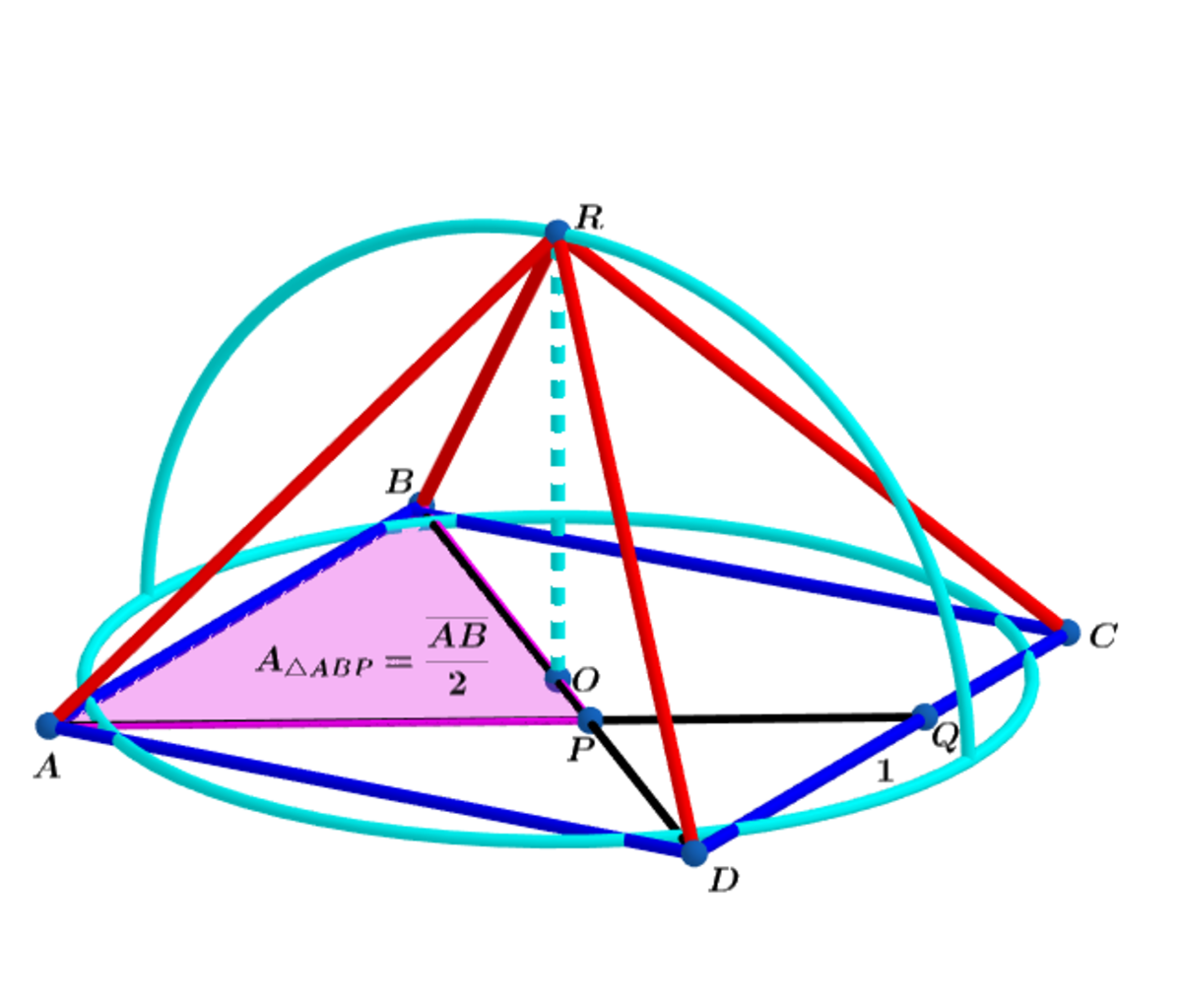
In square base , and intersect at with and the area
.
Let be the center of square and construct a circle centered at whose circumference is equal to the perimeter of the square. Folding the arc of the semi-circle at a right angle, as shown above, the radius of the semicircle becomes the height of the right square pyramid.
Let be the lateral surface area and be the area of the square base.
Find .
The answer is 1.618993.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I provided two solutions for the square base.
Solution using coordinate geometry:
For B D : y = a − x and for A Q : y = a 1 x ⟹ x = a + 1 a 2 ⟹
A △ A B P = 2 ( a + 1 ) a 3 = 2 a ⟹ a ( a 2 − a − 1 ) = 0 a > 0 ⟹
a = 2 1 + 5 = ϕ .
Solution using similar triangles:
Since vertical angles are congruent and A B ∥ C D ⟹ alternate interior angles are congruent ⟹ △ A B P ∼ △ D P Q ⟹
1 a = a − x x ⟹ x = a + 1 a 2 ⟹ A △ A B P = 2 ( a + 1 ) a 3 = 2 a
⟹ a ( a 2 − a − 1 ) = 0 a > 0 ⟹ a = 2 1 + 5 = ϕ
Let O R = r ⟹ 2 π r = 4 ϕ ⟹ r = π 2 ϕ
Let T be the midpoint of A D ⟹ O T = 2 ϕ
In △ R O T the slant height is s = π 2 4 ϕ 2 + 4 ϕ 2 = 2 π ϕ 1 6 + π 2 ⟹
A s = π ϕ 2 1 6 + π 2 ⟹ A □ A s = π 1 6 + π 2 ≈ 1 . 6 1 8 9 9 3 .