Square ratios
The blue square touches each side of the largest square, filling 5 0 2 9 of it.
Each of the 4 red squares at the corners of the largest square touch the blue square.
The fraction of the largest square that is red is b a , where a and b are positive coprime integers.
What is a + b ?
The answer is 2941.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
The problem stated that"The fraction of the largest square that is red is a/b. I took that to mean "all that is red" divided by "large grey square". Not just one red square, but all four. Not 441, but 1764. So couldn't divine the answer without doing a little mind reading.
Log in to reply
Yes, the colors of the original diagram were changed, and the wording is a little confusing.
I do not get it. Why is it for all the red squares and not for one?
Log in to reply
You have to interpret "The fraction of the largest square that is red" as "The fraction of the whole diagram that is colored red", so it is for all four red squares.
Struggling to understand the middle step here where you solve for x and y. I follow the rest of it, assuming you found the correct values of x and y.
My attempt at solving: Given: x+y = 1, x^2 + y^2 = 29/50
(x+y)^2 = 1^2
x^2 + y^2 + 2xy = 1
29/50 + 2xy = 1
2xy = 21/50
xy = 21/100
???
Log in to reply
Almost there! From x + y = 1, y = 1 - x, so xy = 21/100 becomes x(1 - x) = 21/100, which is x - x^2 = 21/100 or x^2 - x + 21/100 = 0. Then by the quadratic equation, x = 3/10, and since y = 1 - x, y = 1 - 3/10 = 7/10.
I think this is a very badly worded problem. It suggests that the red squares are of different sizes, and it asks how the largest red square's area compares to the large square. Now I figured out easily that all the red squares must be of the same size, but I simply couldn't give any other meaning to the question. I then solved until I got that the area of one red square is 441/10000, given that the largest square is a unit square, but the answer 10441 was incorrect, although 441 and 10000 are coprimes. I just missed that very last step of multiplying 441/10000 by 4, and it's really annoying, because the sole reason I couldn't get the right answer is because of the wording of the question. Now I understand that they meant "the fraction of the largest square compared to everything colored red", and the answer to that is 2500/441, add those number and you get 2941, which is the correct answer. Note that English is not my native language, but I think there are many people here with a native language other than English, so maybe the problem should be worded better. Like, "The red squares fill a/b of the largest square, where a and b are coprimes. What is a+b?"
a "badly worded" problem??? it's a very soft way of saying it! SHOW ME, at what point in the text i should guess that it is asked to find the area of FOUR (!!!!!!!) red squares together????? it isn't mentioned anywhere!! AUTHORS, PLEASE CORRECT THE TEXT!!!
Log in to reply
Yeah i spend a month trying to solve this problem!!! And it is never mentioned to find the area
Let the large square be a unit square, the longer leg of the larger gray triangle be G , the shorter leg of the smaller gray triangle be g , and the side of the red square be r . The area of all the gray triangles is given by 2 r G + 2 r g = 2 r ( G + g ) . Because the two triangle legs and two red squares make up one edge of the unit square, this is equal to 2 r ( 1 − 2 r ) . Adding up all the areas inside the unit square gives 2 r ( 1 − 2 r ) + 4 r 2 + 5 0 2 9 = 1 ⟹ 2 r = 5 0 2 1 ⟹ 4 r 2 = 2 5 0 0 4 4 1
I got the area of the blue triangles by just noting they fill half the rectangles between two yellow squares.
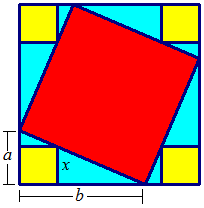 Let area of the large square be 1 hence its side length is also 1. The area of the red square is therefore
5
0
2
9
The area of the triangle inscribing the yellow square (two blue triangles and the yellow square) is
4
1
(
1
−
5
0
2
9
)
=
2
0
0
2
1
.
Let area of the large square be 1 hence its side length is also 1. The area of the red square is therefore
5
0
2
9
The area of the triangle inscribing the yellow square (two blue triangles and the yellow square) is
4
1
(
1
−
5
0
2
9
)
=
2
0
0
2
1
.
Let the short and long side length of the triangle inscribing the yellow square be a and b respectively. Then we have a + b = 1 and:
2 a b a b a ( 1 − a ) ⟹ a 2 − a + 0 . 2 1 = 2 0 0 2 1 = 0 . 2 1 = 0 . 2 1 = 0 Since a + b = 1 Solving the quadraic for a
⟹ a , b = 2 1 ± 1 − 0 . 8 4 ⟹ { a = 0 . 3 b = 0 . 7
Let the side length of the yellow square be x . We note that the large blue triangle is similar to the triangle inscribing the yellow triangle. Therefore, we have:
b − x x 7 x ⟹ x = b a = 7 3 = 2 . 1 − 3 x = 1 0 0 2 1
The area of the four yellow squares is 4 x 2 = 4 × 1 0 0 2 2 1 2 = 2 5 0 0 4 4 1 . Therefore, a + b = 4 4 1 + 2 5 0 0 = 2 9 4 1 .
Why is a+b=1?
Log in to reply
@Ferhat Qqn the whole image is rotationally symmetrical. a and b are the two parts of one side of the large square, so they add up to the side length which is stated to be 1.
For the last 2 mentions of yellow triangle read yellow square...
This could be easily solved in the mind. You move grey triangles making two grey rectangles, leaving blue rectangle in the centre (without touching red area). Then you move blue rectangle down, and then join two red rectangles together making one red square.
Its size can be easily calculated, cause if big square have side length equals 1 , then blue rectangle have side lengths 1 and 5 0 2 9 . So red square have side length 1 − 5 0 2 9 = 5 0 2 1 .
Area equals ( 5 0 2 1 ) 2 , answer is 2 1 2 + 5 0 2 = 2 9 4 1
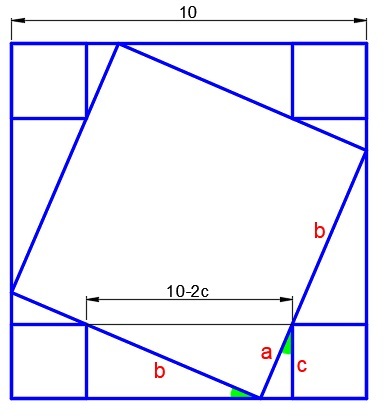 Let the side length of the biggest square be
1
0
. So the area of the biggest square is
1
0
0
. The area of the red square is
5
0
2
9
×
1
0
0
=
5
8
. The side length of the red square is
a
+
b
=
5
8
. By applying similar triangles, we have
Let the side length of the biggest square be
1
0
. So the area of the biggest square is
1
0
0
. The area of the red square is
5
0
2
9
×
1
0
0
=
5
8
. The side length of the red square is
a
+
b
=
5
8
. By applying similar triangles, we have
a c = 1 0 − 2 c b
a b = 1 0 c − 2 c 2 (equation 1)
Let's square a + b = 5 8 . It becomes a 2 + 2 a b + b 2 = 5 8 . This becomes our equation 2. Substituting equation 1 to equation 2, we get a 2 + b 2 = 5 8 − 2 0 c + 4 c 2 . This is our equation 3.
Apply pythagorean theorem,
( 1 0 − 2 c ) 2 = a 2 + b 2
1 0 0 − 4 0 c + 4 c 2 = a 2 + b 2 (equation 4)
Substituting equation 3 to equation 4, we get c = 1 0 2 1 .
The area of one yellow square is ( 1 0 2 1 ) 2 = 1 0 0 4 4 1 .
The area of four yellow squares is 4 × 1 0 0 4 4 1 = 2 5 4 4 1
The fraction required is 1 0 0 2 5 4 4 1 = 2 5 0 0 4 4 1
The desired answer is 4 4 1 + 2 5 0 0 = 2 9 4 1
Let x denote the sidelength of a yellow square and let y denote the ratio of the longer leg to the shorter leg in each triangle (they are all similar, so this is well-defined). Then the largest square has area ( x + x y + y x + x ) 2 = 1 ⟹ y ( 1 + y ) 2 = x 1 and the red square has area ( x + x y ) 2 + ( x + y x ) 2 = 5 0 2 9
This second equation can be rewritten as 5 0 2 9 = x 2 ( y ( 1 + y ) 2 − 2 ) ( y ( 1 + y ) 2 ) = x 2 ( x 1 − 2 ) ( x 1 ) = 1 − 2 x which gives x = 1 0 0 2 1 so the total area of the yellow squares is 4 x 2 = 5 0 2 2 1 2 = 2 5 0 0 4 4 1 and since we defined the area of the largest square to be 1 , this is also the fraction of the largest square that the yellow squares fill. Therefore, the answer is 4 4 1 + 2 5 0 0 = 2 9 4 1
Let x be the side length of the red square and y be the length of the largest square. Equating the area of the blue regions in two different way, ( y − 2 x ) 2 + 4 ( y − 2 x ) x / 2 = ( 2 9 / 5 0 ) y 2 , 5 0 y 2 − 1 0 0 x y = 2 9 y 2 , 2 1 y = 1 0 0 x , 4 x 2 / y 2 = 4 ( 2 1 / 1 0 0 ) 2 = 4 4 1 / 2 5 0 0 , a + b = 2 9 4 1 .

Refer to the above diagram. Let x be the side length of the red square. By similar triangles we get the relation x a − x = b a . Thus x = a + b a b . The side length of the blue square be c . The sides of the blue square forms a right triangle with the sides a and b . Since the side length of the large square is a + b , ( a + b ) 2 c 2 = 5 0 2 9 or ( a + b ) 2 a 2 + b 2 = 5 0 2 9 . Let ( a + b ) 2 = 5 0 (the area of the large square) and a 2 + b 2 = 2 9 (the area of the blue square). This means ( a + b ) 2 − ( a 2 + b 2 ) = 5 0 − 2 9 , which shows that 2 a b = 2 1 or a b = 2 2 1 . The area of red is four times the area of the red square. 4 x 2 = 4 ( a + b a b ) 2 = 4 ⋅ 4 4 4 1 ⋅ 5 0 1 = 5 0 4 4 1 . Since the area of the large square is 50 5 0 4 x 2 = 2 5 0 0 4 4 1 . Just add the numerator and denominator to get 2 9 4 1 .
Let 'c' be the side of large square. Let 'b' be the side of middle square and 'a' the side of small four squares. Then, we have the relation b^2=(c-2a)^2+2a(c-2a)=c(c-2a), Assuming c=10 with (b^2/c^2)=(29/50), we get, a=(21/10), which gives, (4a^2/c^2)=(21/50)^2=441/2500, Therefore, Answer=2941

I am sorry, but I do not know how to make the image smaller.
Let the larger square be a unit square.
We note that x + y = ( 1 − 2 s ) . The area of the four triangles is 1 − 5 0 2 9 = 5 0 2 1 . Therefore, 4 ( s 2 + 2 1 x s + 2 1 y s ) = 5 0 2 1
4 [ s 2 + 2 1 s ( x + y ) ] = 4 [ s 2 + 2 1 s ( 1 − 2 s ) ] = 4 ( s 2 + 2 1 s − s 2 ) = 2 s = 5 0 2 1 So s = 1 0 0 2 1
Finally, 4 s 2 = 2 5 0 0 4 4 1 So the answer is 2 9 4 1

Divide up as in the picture, swap the colors as indicated by the arrow, and you end up with a blue rectangle in the middle and a rectangle at the top and bottom both the height of the red squares. Given that the blue rectangle obtained that way is 29/50 of the height, twice the height of the red square is 1 - 29/50 = 21/50 of the height of the full square. Likewise for the width. The 4 squares form a single square of twice the height and width of a single square, so it is ( 2 1 / 5 0 ) 2 = 4 4 1 / 2 5 0 0 of the total square, and thus the answer is 441 + 2500 = 2941. Done.
Assuming that the length of the largest square is 10,the area of the bule square is 58 accordingly.
The area of the blue square can be presented as (10-2a)
a
2+(10-2a)^2 which equals 58.Then we get a(
5
7
).

Let the side of the larger square be 1 .
⟹ 1 = 2 ( y ) ( 1 − y ) + 5 0 2 9 ⟹ 1 0 0 y 2 − 1 0 0 y + 2 1 = 0 ⟹ y 1 = 1 0 7 and y 2 = 1 0 3 .

Using similar triangles above
⟹ 1 0 x 7 − 1 0 x = 3 − 1 0 x 1 0 x ⟹ x = 1 0 0 2 1 ⟹ A r e d = 4 ( 1 0 0 2 1 ) 2 = ( 5 0 2 1 ) 2 = 2 5 0 0 4 4 1 = b a ⟹ a + b = 2 9 4 1 .
This problem reminds me of deriving the pythagorean theorem using areas.

The area of the square ( a + b ) 2 = 2 a b + c 2 ⟹ a 2 + b 2 = c 2 .
I posted a somewhat similar problem:
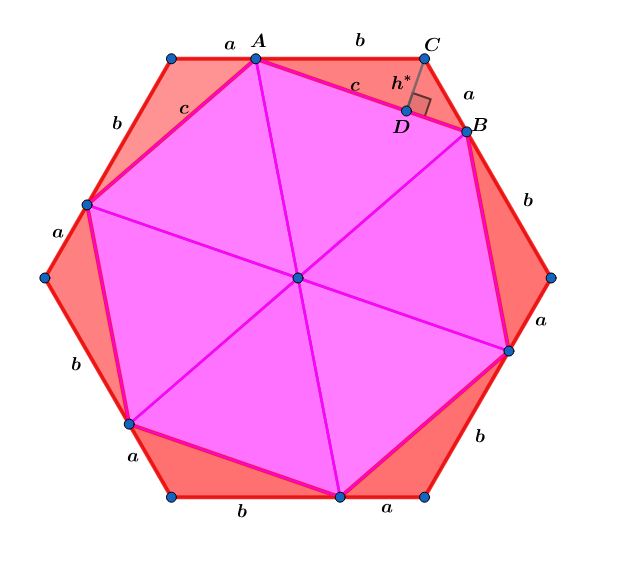
Let the diagram above be extended to a regular n − g o n and A j , where ( 1 ≤ j ≤ n ) , be the area of one of the red triangles.
If lim n → ∞ ∑ j = 1 n A j = π ( a 2 + 2 a b − 1 2 b 2 ) find b a .
The area of what simple closed curve does ∑ j = 1 n A j converge to?
The big square is four congruent right triangles plus the red square. Call the sides of those four congruent right triangles a , b , c , with c the hypotenuse. Then ( a + b ) 2 c 2 = 5 0 2 9 , but c 2 = a 2 + b 2 by Pythagoras, so ( a + b ) 2 a 2 + b 2 = 5 0 2 9 and subtracting both sides from 1 gives ( a + b ) 2 2 a b = 5 0 2 1 . Now the side length x of the four yellow squares is half the harmonic mean of a and b , x = a + b a b , and the ratio of the areas of the four yellow squares to the big square is ( a + b ) 2 4 ( a + b a b ) 2 = ( a + b ) 4 4 ( a b ) 2 . But this is just the square of the quantity we looked at above. So the answer is ( 5 0 2 1 ) 2 = 2 5 0 0 4 4 1 , and the answer is 2 9 4 1 .
Another way to get the dimensions of the grey triangles:

Label the diagram as per David Vreken's solution.
Let the large square be a unit square. The area of the blue square is 5 0 2 9 , so the area of the four grey triangles is 5 0 2 1 . Thus, by symmetry, the area of the four blue triangles is 5 0 2 1 . Thus, the area of the small inner blue square is 5 0 8 = 2 5 4 . Thus its side length is 2 5 4 = 5 2 . Looking at the sum of vertical measures, the length of the inner blue square is 1 − 2 x . Thus 1 − 2 x = 5 2 ⇒ x = 1 0 3 . Now y = ( x ) + ( 1 − 2 x ) = ( 1 − x ) = 1 0 7 .
From here proceed as per David Vreken's solution to find the side length of the red squares and thus their area.
Let S = side of large square, d = side of red square, t = side of yellow square, x = distance from a corner of large square to closest point where red squae touches large square. Then, d^2 = x^2 + S - x)^2 gives a quadratic in x. Substituting d^2 = (29/50)S62, and solving the quadratic for x, x = 3S/10. The Blue area in one corner = (1/2)(t)(x - t) + (1/2)(t)(S - x - t). Then the total Blue area is (multiplying by 4 and simplifying), 2tS - 4t^2.We have Blue area = 2tS - 4t^2, yellow area = 4t^2, red area = (29/50(S^2, and total area = S^2. Equating the sum of area to S^2, we have 2tS =(21/50)S^2, or t = 21S/100. The ratio of interest is 4t^2/S62, which is 4*441/10000, which reduces to 441/2500, and 441 + 2500 = 2941. Ed Gray

Let x be the length of the smallest side of the smaller blue triangle plus the length of one of the sides of the yellow square, let y be the length of the medium side of the larger blue triangle plus the length of one of the sides of the yellow square, and z be the length of one of the sides of the yellow square, as shown below. Also, let the large square be a unit square, so that the red square has an area of 5 0 2 9 and therefore a side length of 5 0 2 9 .
Then by Pythagorean's Theorem, x 2 + y 2 = 5 0 2 9 , and as a unit square, x + y = 1 , Solving the system of equations for x < y gives x = 1 0 3 and y = 1 0 7 .
By similar triangles, y x = y − z z , or 1 0 7 1 0 3 = 1 0 7 − z z , which solves to z = 1 0 0 2 1 .
This means that the ratio of the area of four yellow squares to the area of the large square is 1 4 z 2 = 1 4 ( 1 0 0 2 1 ) 2 = 2 5 0 0 4 4 1 , so a = 4 4 1 and b = 2 5 0 0 , and a + b = 2 9 4 1 .