Square root!
True or False?
If ( a − b ) × ( a − b ) = ( c − b ) × ( c − b ) , then it must be true that a = c .
Bonus: If you think it's true, prove it; if you think it's false, find a counterexample.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
59 solutions
I don't quite follow the different equivalents.
Log in to reply
Two possibilities:
a − b = c − b ⟹ a = c
a − b = − ( c − b ) ⟹ a − b = − c + b ⟹ a = 2 b − c
How can I add counterexample??
Log in to reply
take the formular from above and fill in any 2 of the three numbers. Lets take b=2 and c=3 this will give us: a = 2*2 - 3 = 1
So basically it means either a=c or a,b,c are in arithmetic progression.
(a-b)^2 ) = (c-b)^2 a^2 -2ab + b^2 = c^2 -2cb + b^2 a^2 -2ab = c^2 - 2cb -b^2+ b^2 a^2 -2ab = c^2 - 2cb a^2 = c^2 -2cb + 2ab c^2 = a^2 +2cb -2ab a^2 + c^2 = c^2 + a^2 0 = 0 so a = c
Take ( 2 − 3 ) 2 and ( 4 − 3 ) 2
( 2 − 3 ) 2 = ( − 1 ) 2 = 1 and ( 4 − 3 ) 2 = 1 2 = 1
Here 2 is not equal to 4, so this is an example for the above statement to be wrong.
If we take ( 2 − 3 ) 2 and ( 2 − 3 ) 2 ,
Now this an example for the above equation to be true.
So, the correct answer would be True, sometimes(or False).
Moderator note:
Note when featuring the problem we decided to simplify it into a True/False, so it isn't necessary to decide cases where the statement works and cases where it doesn't. It's now, simply using the logic of an if-then statement, the conclusion always follows when the conclusion is true (making the if-then statement true) or the conclusion doesn't always follow (making the if-then statement false).
So, can we add an extra option ""sometimes true". Or can we add a condition that a , b , c > 2
Log in to reply
If a,b,c > 2, we can still find a counter-example.
a = -10 b = 10 c = 30 this also works and here a,b,c > 2
In mathematics, "sometimes true" means "not true". For example, the statement "the product of any two natural numbers is even" is false, even though sometimes such a product is even.
The question asks for, " must be true." So if the answer is sometimes true, then you should still answer the question as "false" because it's not always true.
As Laura said, the logics of the question make the only correct answer „FALSE”.
one single counter example is enough to prove that the statement is false, in other words, to say that it is "sometimes true and sometimes false" is to say that it is false.
@Vaibhav Priyadarshi , Please don't ask a confusing question the answer of which is ambiguous.
Counterexample: b = 0 , a = − c ( a = 0 )
Then, ( a − b ) × ( a − b ) = a 2 = ( − c ) 2 = c 2 and obviously ( c − b ) × ( c − b ) = c 2
a = 2 b = 4 c = 6
(2 - 4) x (2 - 4) = (6 - 4) x (6 - 4)
-2 x -2 = 4
2 x 2 = 4
Log in to reply
Nice and clear explanation
Could this be put into more abstract terms?
In other words, can we derive a full equivalence class for these values in the equation?
Is this the only class of counter example possible?
If we expand the parentheses:
( a − b ) 2 = ( c − b ) 2 ⟹ a 2 − 2 a b + b 2 = c 2 − 2 b c + b 2
a 2 − c 2 = 2 a b − 2 b c
( a + c ) ( a − c ) = 2 b ( a − c ) ⟹ a + c = 2 b
Although the statement holds for a = c it also holds for a + c = 2 b .
Piero, in order to get a+c=2b, you need to simplify both sides dividing by (a-c). You can only divide it as long as a is different than c.
The easiest solution is to take a = 1, c = -1 and b = 0. Then 1 x 1 = -1 x -1 = 1
( a − b ) 2 = ( c − b ) 2 ( b − a ) 2 = ( c − b ) 2 ⟹ 2 b = a + c (A.M) shows that a = c . Hence the statement we have is false . The statement will be true either a = b or b = c .
( a − b ) 2 = ( c − b ) 2 doesn't implies a − b = c − b however, ∣ ( a − b ) ∣ = ∣ c − b ∣ .
Put a=2 and b=1 and c=2 so according to equation 1=1
If we take b = 0, a and c may not necessarily be equal, as if a^2 = c^2, then a = c OR a = -c.
We have:
( a − b ) 2 a 2 − 2 a b + b 2 a 2 − c 2 − 2 b ( a − c ) ( a − c ) ( a + c − 2 b ) = ( c − b ) 2 = c 2 − 2 c b + b 2 = 0 = 0
So, it's either a = c or a + c = 2 b and thus the answer is False.
It's (a-b)^2 and you wrote the formula of (a+b)^2
We have (a-b) (a-b) = (c-b) (c-b)--------eq1, This simplifies to a^2-2ab=c^2-2bc. Solving further we get the relation a+c=2b. This clearly indicates that a,b,c are in arithmetic progression. Therefore eq1 is true for any three consecutive terms in an arithmetic progression . Thus, this implies that eq1 is not only true for a=c but also for other values of a and c. For example, let the A.P. be 2,5,8 where a=2, b=5 and c=8, Now, (2-5) (2-5)=(8-5) (8-5) 9=9 Since LHS=RHS, the above equality holds true.
Let us take a = 5 , b = 3 , c = 1
( a − b ) 2 = ( 5 − 3 ) 2 = 2 2 = 4
( c − b ) 2 = ( 1 − 3 ) 2 = ( − 2 ) 2 = 4
Here, a = c but ( a − b ) × ( a − b ) = ( c − b ) × ( c − b )
If we observe carefully here the condition a = c is satisfied only when a,b,c are in A.P .
Now put a = a, b = a + d, c = a + 2d
When we substitue the above in ( a − b ) × ( a − b ) = ( c − b ) × ( c − b ) we get d 2 = d 2 .
This tells that our assumption that a,b,c are in A.P is true. So, it is obvious that a = c .
Let A = 1, B = 0, C = -1. The result will be 1 = 1 through the formula, yet a != c.
counter example, a=1, b=2, c=3.
Not necessarily a=c because:
(a-b)^2=(c-b)^2 ; (a-b)^2-(c-b)^2=0 ; [(a-b)-(c-b)][(a-b)+(c-b)]=0 ; (a-c)(a+c-2b)=0 therefore either a-c=0 or a+c-2b=0 where we get:
a=c or a=2b-c.
So the answer is false.
Here is a proof by counterexample
Let b = 0
Our equation then simplifies to
a
2
=
c
2
Which has a = − c as a solution.
Therefore, a is not necessarily equal to c in all cases. Thus, the answer is False .
(7-3)(7-3)=(-1-3)(-1-3) and 7 = -1
( a − b ) 2 = ( c − b ) 2 = > ( 2 − 3 ) 2 = ( 4 − 3 ) 2 = > ( − 1 ) 2 = ( 1 ) 2 = > a = 2 b − c or ( a − b ) 2 = ( c − b ) 2 = > m 2 = − m 2 therefore, a = c is not required since we can achieve m and -m with different values for a and c.
For a counterexample, simply let b = 0 and we have the classic assumption where two squares equal means their square roots are also equal. Clearly FALSE.
This is the same as the top solution I just wanted to point out that the simplified equation is ±(a - b) = ±(c - b) NOT (a - b) = ±(c - b), either side of the equation may be positive or negative since the square root must be taken of both sides.
Basically the question asks us if the f ( x ) = ( x − b ) 2 is an injective function or not. It can simply be checked graphically by drawing y = ( x − b ) 2 for an arbitrary value of b and if any line parallel to x-axis, y = k cuts the graph at two or more points it's not an injective function.
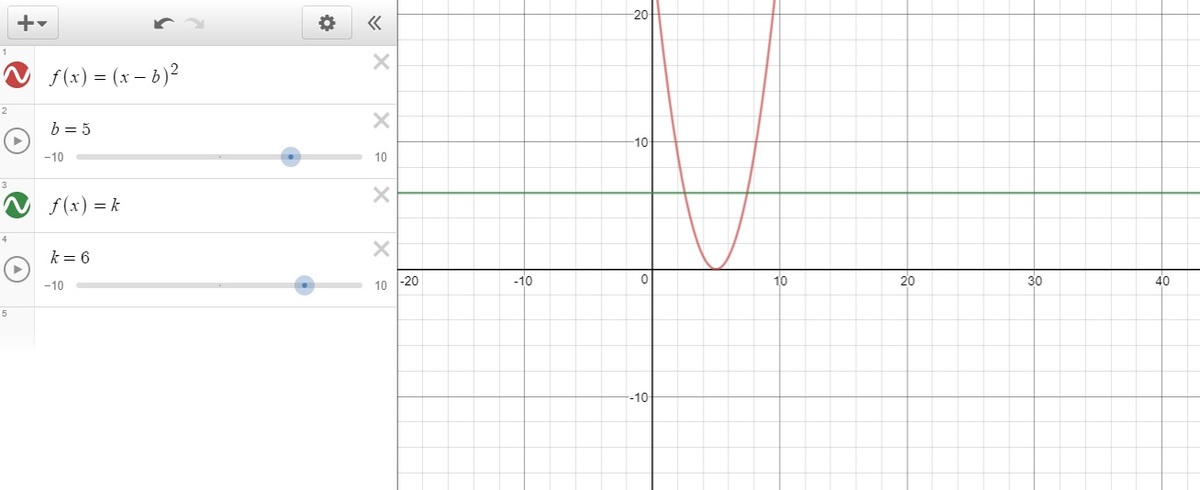
This clearly shows that f ( x ) = ( x − b ) 2 is not an injective function hence for the original question, if ( a − b ) × ( a − b ) = ( c − b ) × ( c − b ) the statement a = c may not be true.
The only "exception" is the case ( a − b ) × ( a − b ) = ( c − b ) × ( c − b ) = 0 , where the statement a = c = b must be true
When it comes down to it, I was able to simplify to: a^2 - a = c^2 - c
I used a=3, then solved for what c could be. It could be 3 OR -2. Therefore, since one solution was found, then statement is false.
if you divide left and right parts by (a+b) would you get that a is not -b?
Log in to reply
Max, you cannot simplify the right side with a-c, because this can ONLY be done as long as a is not equal to c.
If a=c than you get that c may be any number you want.
Log in to reply
Max, if a=c then you will get 0 at denominator, which makes it impossible.
Counter example: b = 0 , a = − c = 0 .
( a − b ) ( a − b ) = ( c − b ) ( c − b ) , let a = 2 and b = 3 results in an imaginary solution
(2-1)x(2-1) = (0-1)x(0-1)
If a = c or a + c = 2b then the above equation is true. Therefore it is not necessary that a must be equal to c
| ( a − b ) 2 = ( c − b ) 2 | N o w . . . L e t : a = c . . . | |
| a 2 − 2 a b + b 2 = c 2 − 2 b c + b 2 | ( a − b ) 2 − > ( c − b ) 2 | |
| a 2 − 2 a b = c 2 − 2 b c | ( c − b ) 2 = ( c − b ) 2 | |
| a 2 − c 2 = 2 a b − 2 b c | ( c − b ) 2 − ( c − b ) 2 = 0 | |
| a 2 − c 2 = 2 b ( a − c ) | . . . I t i s f a l s e . . . | |
| a − c ( a + c ) ( a − c ) = 2 b | ||
| a = 2 b − c |
If a=b+x and c=b-x the statement is always true, no matter the value of x.
Quadratic equations tend to have to different roots/solutions, due to their u-shaped graph
(a - b)² = (c - b)²
-
a² - 2ab + b² = c² - 2cb + b²
-
a² - c² = 2ab - 2cb
-
a² - c² = 2b(a - c)
-
a − c a ² − c ² = 2b
-
( a − c ) ( a + c ) ( a − c ) = 2b
-
a = 2b - c
since the equation could be seen as x 2 = y 2 any values that satisfy a − b = − ( c − b ) or a = 2 b − c will work.
The answer must be false on technicality, as you reduce the statement to a^2 - 2ab = c^2 - 2cb. You can use the quadratic formula to show that c will have 2 values, therefore not always equal to a.
a=1 b=2 c=3 a not equal to c
( a − b ) × ( a − b ) is the same thing as ( a − b ) 2 , and as we know the square of a positive number is the same as the square of it's negative value. So ( a − b ) 2 = ( c − b ) 2 is possible if ( a − b ) = − ( c − b ) .
Example:
( 2 − 3 ) = − ( 4 − 3 )
− 1 = − ( 1 )
− 1 2 = 1 2
a^2 - b^2 = c^2 - b^2, a^2 = c^2, a = c or a = - c
Simply take b=0 and a=1 so b may be equal to-1 hence statement is false
Given that a minus b square is equal to C minus b square . Now here 2 cases arise : Case 1: A minus b = C minus b in this case the value of a is equal to that of c Case 2: A minus b = negative of C minus b that is a minus b = B minus C it implies that A plus c Is equal to twice of B so in this case a is not equal to c. Example : A is equal to 1 B = 2 and C = 3
Take b = 0 , since it doesn't matter for the purposes of finding a counterexample.
Now we just have
a 2 = c 2
But we know that square roots can have both positive and negative solutions, so taking the square root of both sides produces:
± a = ± c
Because the signs can differ on both sides, a doesn't have to equal c -- it can also be the negative of c, and when they're squared, they become equal.
Example:
a = 3 , b = 0 , c = − 3
3 2 = ( − 3 ) 2
If a is equal to 2 and b is equal to 1 then the result of 1x1 (that is the end of the a-b count) will be 1. But if c is 0 then the solution will be (0 - 1) x (0 - 1) that is (-1) x (-1), this is equal to 1 so the afirmative inst always right
if a = -2 and b = 2 then the answer to the first is 16. then C could be 6 and b is again 2 then the answer is 16
Counter example: If you let a=0 then you can show that c=2b. so a=0 b=1 c=2
If b=0 we end up with a² = c² which can be achieved by 1² = (-1)², here a =/= c therefore the above statement does not hold true.
If a^2 - 2ab + b^2 = c^2 -2cb + b^2, Then a^2 - c^2 = 2ab – 2cb, and a^2 - c^2 = 2b (a – c). So, (a + c)(a – c) = 2b (a – c), Thus a + c = 2b, that is, a = 2b - c
At this point, it is clear that the expression can't be simplified anymore. Hence, a ≠ c
This is not correct explanation.
Counter example is (3-4) (3-4)=(11-10) (11-10).... There are a lots of example such that a is not equal to c.
It is not a counterexample. Question is asking for (a-b)(a-b)=(c-b)(c-b). But you have taken two values of b which we can't take because a particular variable denotes Same value in same condition.
- a x - a its equal to a x a, then a is not equal to -a
If a=c then that means there would be no reason to have a c unless we were comparing natural to ordinals which in a logical sense would not be logical you could be taking absolutes but no one like those
( a - b )^2 = ( c - b )^2
So how about using the following:
a = -2
b = 4
c = 10
Would make: ( -2 -4 )^2 = ( 10 - 4 )^2
-2 -4 = -6
-6^2= 36
10 - 4 = 6
6^2 = 36
36 = 36
It's a simple matter of - x - = +
(a)(a)+(a)(−b)+(−b)(a)+(−b)(−b)+−b2+2bc+−c2
=a2+−ab+−ab+b2+−b2+2bc+−c2
Combine Like Terms:
=a2+−ab+−ab+b2+−b2+2bc+−c2
=(a2)+(−ab+−ab)+(b2+−b2)+(2bc)+(−c2)
=a2+−2ab+2bc+−c2
Conjugates are indistinguishable for polynomials of real coefficients. Simple example is b=0 a=i c=-i
Imagine a parabola ( x − b ) 2 , it is symmetric around x = b so for every d > 0 there will be two values of x where ( x − b ) 2 = d is satisfied
Take a = 1 ; b = 2 ; c = 3 (where a!=c) Put in above equation: ( 1 − 2 ) ∗ ( 1 − 2 ) = ( 3 − 2 ) ( 3 − 2 ) which implies that: ( − 1 ) 2 = ( 1 ) 2 Therefore: 1 = 1
let a =1, c =0, b= .5. then a -b = .5 and c -b = -.5, and (a -b)x(a -b) = .25, and (c - b)x(c - b -.5x-.5 = .25Ed Gray
- a2 - 2ab + b2 = c2 - 2bc + b2
- a2 - 2ab = c2 - 2bc
- a(a - 2b) = c(c - 2b)
- a = c(c - 2b)/(a - 2b)
- a /= c
If ( a − b ) ( a − b ) = ( c − b ) ( c − b )
then ( a − b ) 2 = ( c − b ) 2
( a − b ) = ( c − b ) 2
( a − b ) = ± ( c − b )
if taken as positive
( a − b ) = + ( c − b )
a − b = c − b
a = c − b + b
a = c
and if taken as negative
( a − b ) = − ( c − b )
a − b = − c + b
a = c + b + b
a = 2 b − c
so value of a can be 2 b − c too. This makes the statement false.
LS (a-b) X (a-b) = (c-b) X (c-b) RS
a^2 + 2ab + b^2 = c^2 + 2cb + b^2
Subtract (b^2) and (c^2) from both sides and add (2ab) to both sides so that we get:
a^2 - 2ab + c^2 + b^2 - b^2 = c^2 - c^2 - 2cb + 2ab + b^2 - b^2
Once you cancel like terms you should end up with:
a^2 - c^2 = 2ab - 2cb
(a^2 - c^2) is a difference of squares and as such can be re written as:
(a+c) X (a-c) = 2b(a-c)
If we divide (a-c) from both sides we end up with:
a+c = 2b
If we wanted to isolate for either a or c we would end up with either (a = 2b - c) or (c = 2b - a). Since (c = 2b - a) =/= (c = a) the assertion is false.
The equation c=2b-a makes this equation true with infinite solutions.
Let's find out if this is true or false.
If (a - b) × (a - b) = (c - b) x (c - b), then we have:
( a − b ) 2 = ( c − b ) 2 , so
∣ a − b ∣ = ∣ c − b ∣
Now we can divide the problem in 2 cases:
(a - b) = (c - b) or (a - b) = (b - c)
In the first case, we conclude that a = c, so the statement would be true.
In the second case, however, we conclude that a - 2b = c, which is only true when b = 0, so the statement is false.

Relevant wiki: Quadratic Equation
( a − b ) 2 = ( c − b ) 2 ⟹ ( a − b ) = ± ( c − b ) ⟹ a = c OR a = 2 b − c .