Square roots galore

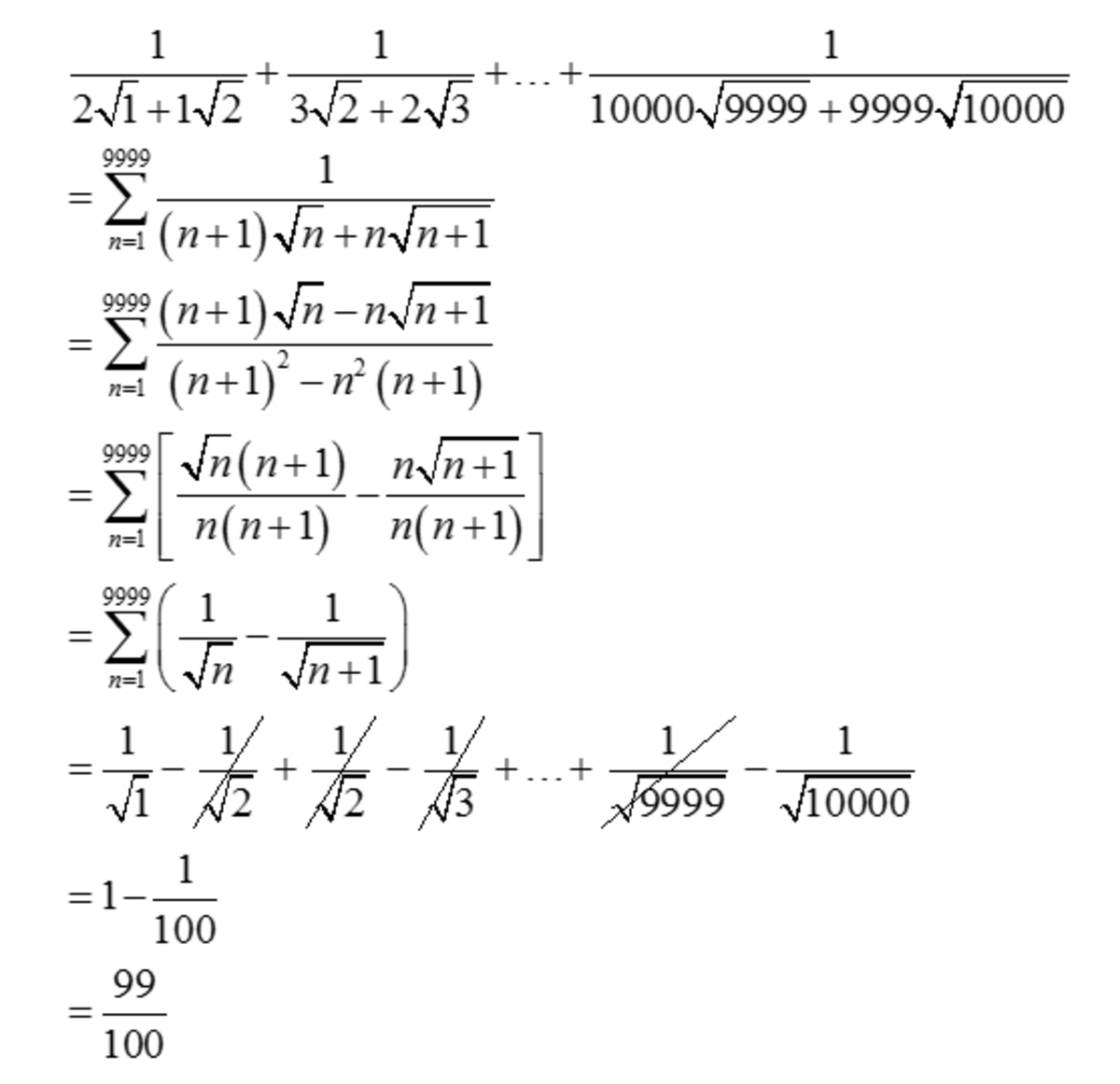
Let $\displaystyle a_n=\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1}}$ . Then the sum we are looking for is equal to $\displaystyle\sum_{n=1}^{9999} a_n$ . We can express $a_n$ as $\frac{1}{\sqrt{n.(n+1)}.(\sqrt{n}+\sqrt{n+1})}$ .Then, multiplying the numerator and denominator by $\sqrt{n+1}-\sqrt{n}$ we would get $a_n= \frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n.(n+1)}}=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}$ .So our series telescopes and our answer is $1-\frac{1}{\sqrt{10000}}=\boxed {0,99}$

P.S.:Thank you Calvin for correcting the problem and adding a picture to it :D

WRITE BACK THE EQUATION AS IN (1/K) +(1/(K+1)) FORM TO MAKE IT TELESCOPING SERIES, AND SUMMATION OF TELESCOPING SERIES IS UNITY

Using Python

take first term which is equal to 1/sqrt of 1- 1/sqrt of 2 , same as second term is 1/sqrt of 2-1/sqrt of 3 and so on. therefore finally we get 1/sqrt of 1-1/sqrt of 10000= 0.99