square & semicircle
Given on the figure , a square ABCD of unit area , CE is tangent to the semicircle of diameter AB at E . If the area of the triangle AED =
n
1
, n is an integer , find n ?
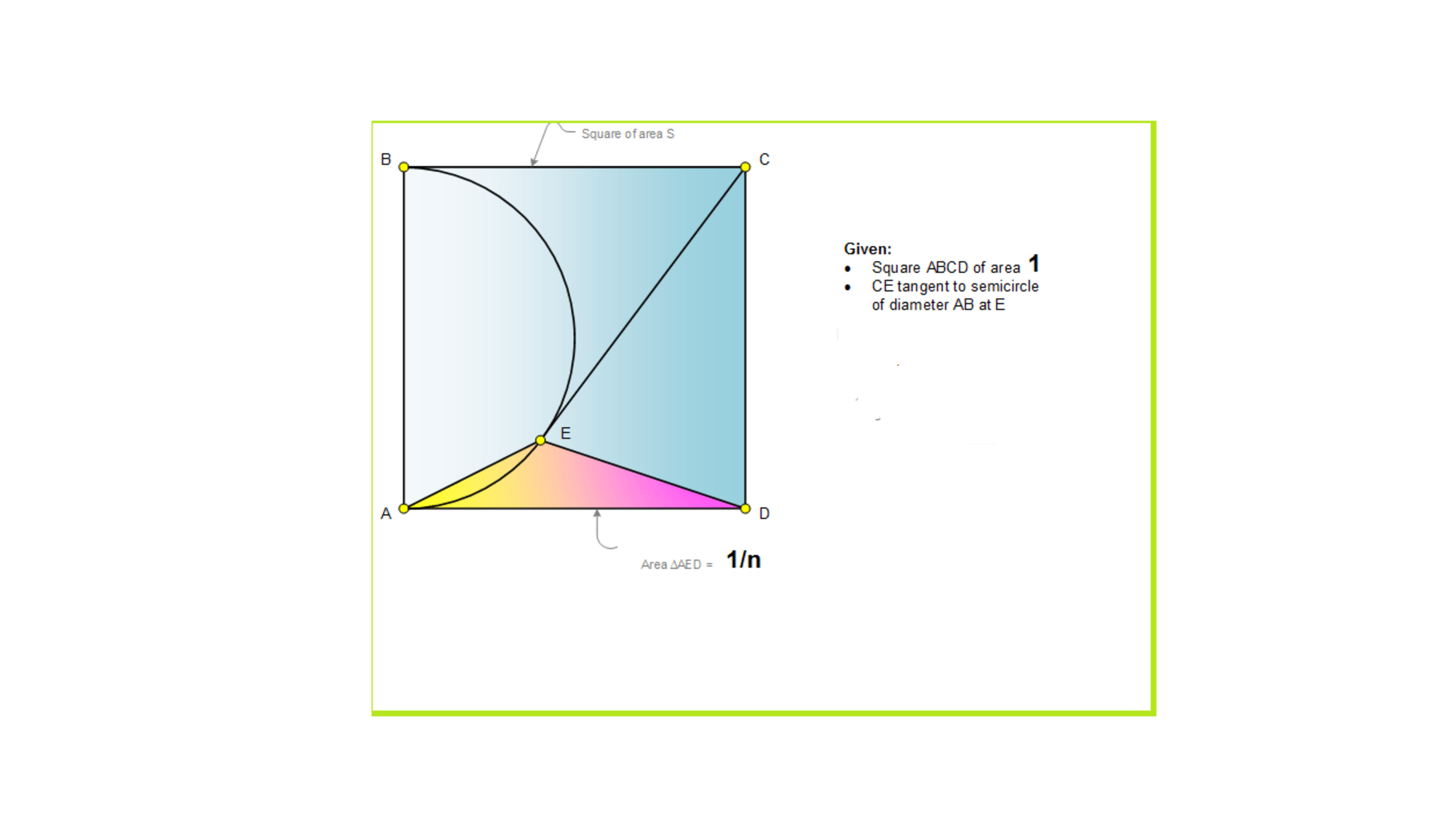
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This question looks like the sort of thing I'd see on my maths HSC, so I think I'll do a full proof for practice, along with some other comments.
Construct the lines CM, EM, EN and EO where M is the midpoint of AB, N lies on AB so that EN is perpendicular to AB and O lies on AD so that EO is perpendicular to AD:
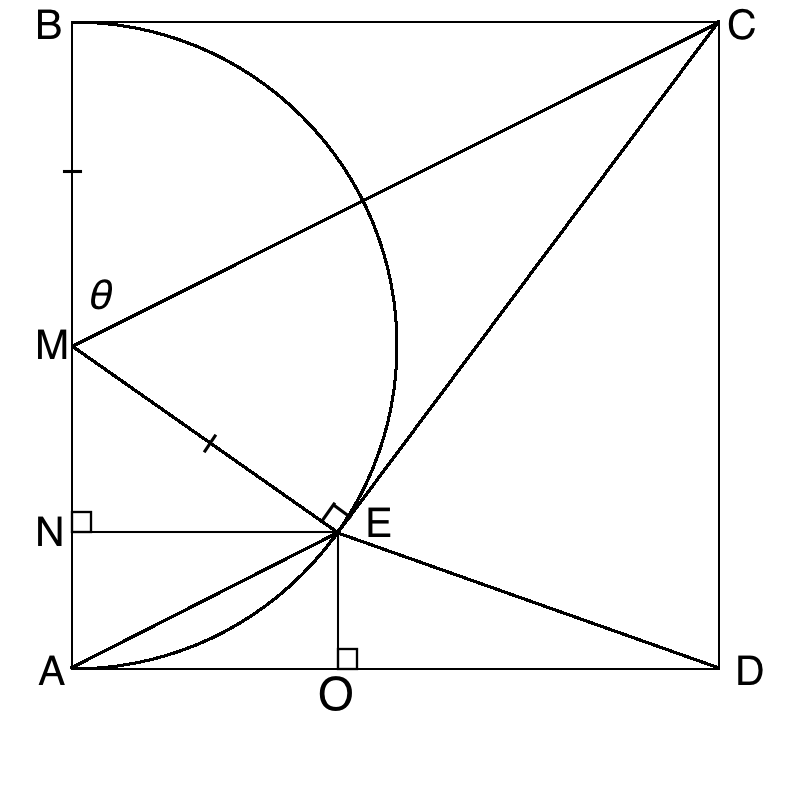 Note that the sides of the square are all 1, so AM and BM are both 1/2. ME is also 1/2, as the semicircle has a constant radius of 1/2.
Note that the sides of the square are all 1, so AM and BM are both 1/2. ME is also 1/2, as the semicircle has a constant radius of 1/2.
l e t ∠ B M C = θ
tan θ = 1 / 2 1 = 2
θ = arctan 2 ( w h e r e θ i s a c u t e )
Now we prove congruency of the triangles BCM and ECM to find angle CME, and in turn angle NME:
∠ C B M = ∠ C E M = 9 0 ∘
M C i s c o m m o n
B M = E M ( r a d i u s o f s e m i c i r c l e )
∴ △ B C M ≡ △ E C M ( R H S )
This is one of the few times in my entire study of mathematics that I have found the "Right angle, Hypotenuse, Side" rule useful.
∴ ∠ C M E = θ ( c o r r e s p o n d i n g a n g l e s i n c o n g r u e n t t r i a n g l e s a r e e q u a l )
∴ ∠ N M E = 1 8 0 ∘ − 2 θ ( a n g l e s o n a s t r a i g h t l i n e s u m t o 1 8 0 ∘ )
Now we can use angle NME to find the length of NM, which will help us find the perpendicular height, EO, of the triangle we want.
i n △ E M N : cos ( 1 8 0 ∘ − 2 θ ) = E M N M
cos ( 1 8 0 ∘ ) cos ( 2 θ ) + sin ( 1 8 0 ∘ ) sin ( 2 θ ) = 1 / 2 N M
− 1 cos ( 2 θ ) + 0 sin ( 2 θ ) = 2 N M
1 − 2 cos 2 ( 2 θ ) = 2 N M
N M = 2 1 − cos 2 θ
There are several techniques to simplify inverse trig functions inside normal ones. Here, I do it algebraically. There should be no issues with negatives, as theta is acute.
N M = 2 1 − sec 2 θ 1
= 2 1 − 1 + tan 2 θ 1
= 2 1 − 1 + ( tan ( arctan 2 ) ) 2 1
= 2 1 − 1 + 2 2 1
= 1 0 3
A N = A M − M N = 2 1 − 1 0 3 = 5 1
E O = A N = 5 1
Now that we know the length of the base and the perpendicular height of triangle AED, we can find n:
A r e a = 2 1 b h
n 1 = 2 1 ( 1 ) ( 5 1 )
n 1 = 1 0 1
n = 1 0
∠ B C E = 2 × a r c t a n ( 2 1 ) ≈ 5 3 . 1 3 ∘
Distance from point E to the top = s i n ( 5 3 . 1 3 ∘ ) = 0 . 8
Distance from point E to the bottom = 1 − 0 . 8 = 0 . 2 = 5 1
Area of △ A E D = 2 1 × 1 × 5 1 = 1 0 1