Square squeeze

To maximize the area of the square, we'll maximize $BD=AB+BC$ .

We know that $AC=\sqrt{2}$ . So if we define $x=AB$ we get $BC=\sqrt{2-x^2}$ and $BD= x+\sqrt{2-x^2}$ .

Setting first derivative equal zero will give us $\frac{x}{\sqrt{2-x^2}}=1$ which is true for $x=1$ .

That means the largest square has $AB=BC=1$ and a side $BD=2$ .

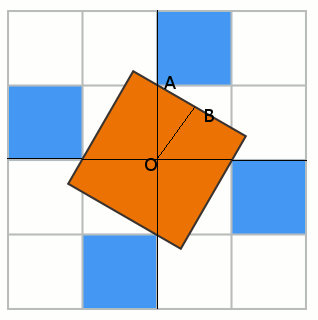
OK, let's add some grid lines to the middle. Note that the center of the square is at the intersection of the gridlines (by symmetry) - call this point $O$ . Let $A$ by the grid point above $O$ and let $B$ be the midpoint of the square's side closest to $A$ . And let $\theta$ be the measure of the angle $\angle AOB$ . Note that $OA = 1$ and $OB = \cos \theta$ . Since $OB$ is half the width of the square we see that the square's area is $4 \times OB^2$ which is $4 (\cos^2 \theta)$ . This value is maximized when $\cos \theta = 1$ , which means $\theta = 0$ , .i.e when the square is flush with the gridlines.

By symmetry, two opposite sides of the square will touch the corners indicated in the figure. Since the distance between these corners is $2$ , then the largest possible square you can fit in there will be $2 \times 2$ . If you rotate the square as shown, the area of the square will only be smaller, since then a line segment connecting two opposite blue squares will go diagonally through the square and will have a distance of $2$ , so the length/width of the square would be less than $2$ .

Therefore, the area of the largest orange square would be: $2 \times 2 = \boxed4$

Imagine the orange square sitting unrotated and covering the four middle squares. In this position it has an area of 4. Now rotate it to a new position and adjust its size so it nestles between the blue squares as shown. Now examine the diagram as drawn by Geoff. As it rotates to the new position the orange square looses four white right angled triangles and gains four orange triangles. The orange triangles are similar to the white ones but smaller, and so the area has been reduced.

The orange triangles are smaller because their hypotenuses are less than a grid unit (just look at the diagram!), while the white hypotenuses are longer than a grid unit (because one of the other sides of the white triangles is a grid unit).

Done.